Модели отказов при прогнозировании технического состояния
Модели, отображающие условия взаимодействия, протекающие во времени, приобретают наглядную форму, если до формализованного описания представлять их в графической форме. Формализованная схема, представлення в графической форме, позволяет установить зависимости между факторами, оказывающими влияние на протекание процесса, приводящего к отказу (аварии, катастрофе) между параметрами объекта и действующими загрузками, соотношение между внутренними характеристиками объекта и внешней среды.
Для простоты геометрической интерпретации моделей воспользуемся методом главной компоненты и будем изображать на графиках лишь одно определяющее свойство объекта –внешнюю нагрузку y, воплощающую в себе факторы условий эксплуатации, ведущие к отказу и его внутреннюю сопротивляемость σ относительно рассматриваемых факторов.
Простейшими случаями графических изображений моделей отказа (или моделей оценивания надежности) являются модели, когда сопротивляемость объекта не зависит от времени. В таких случаях говорят, что объект не стареет.
1. На рисунке 3.2, a зображена графическая модель для случая, когда сопротивляемость σ(t) = σ0 = const – неслучайная величина, не изменяющаяся во времени, а нагрузка y – случайная величина не зависящая от времени.
Рассматриваемый случай представляет собой нагружение объекта случайной статической нагрузкой. Критерием отказа является неравенство y0>σ0.. Исход подобного взаимодействия является неопределенным лишь в момент приложения нагрузки, а длительность ее действия не влияет на исход нагружения.
2. Сопротивляемость неслучайная величина σ(t) = σ0,а нагрузка y(t) – случайная величина, зависящая от времени, т.е. случайный процесс (рис. 3.2, б).
Характер зависимости случайной величины y(t) от времени функциональный: нагрузка независимо от ее начальной величины линейно возрастает со временем. Условием (критерием) отказа является привышение нагрузкой величины сопротивляемости: y(t)>σ0. Неопределенность момента времени появления отказа связана с неопределенностью исходного значения нагрузки.
3. Сопротивляемость – случайная величина σ0, не зависящая от времени, а нагрузка y(t) – случайная величина, линейно зависящая от времени (возрастающая или убывающая). Условие отказа y(t)>σ0. Неопределенность момента наступления отказа (времени безотказной работы) зависит как от случайности сопротивляемости, так и от неопределенности величины нагрузки (рис. 3.2, в).
4. Сопротивляемость – неслучайная величина σ0, а нагрузка - случайный стационарный процесс y(t). Условие отказа y(t)>σ0. Такую модель отказа называют иногда моделью «параметр – поле допуска», что соответствует выходу случайной изменяющейся во времени нагрузки y(t) за пределы установленного
| t |
| σ(t), y(t) |
| σ |
| S |
| φy(t)(y) |
| σ(t), y(t) |
| φy(y) |
| t |
| φy(t)(y) |
| S |
а б
| σ(t), y(t) |
| σ |
| t |
| φy(t)(y) |
| φσ(y) |
| σ(t), y(t) |
| σ |
| t |
| y(t) |
в г
| σ(t), y(t) |
| t |
| φσ(y) |
| t y(t) |
| σ(t), y(t) |
| σ |
| t y(t) |
| φy(y) |
д е
Рис. 3.2 Графические модели отказов без учета старения сопротивляемости: а, б, в, - нагрузка - случайная величина; г, д, е – нагрузка - случайная функция времени
одностороннего (или двустороннего) поля допуска. Подобный отказ может являться как физическим, так и условным, поскольку условие относительно границы поля допуска σ0 может быть сформировано субъектом, использующим объект по назначению.
Эта модель соответствует расчетной схеме, так называемой параметрической надежности, когда под нагрузкой понимается некоторый изменяющийся параметр объекта, а под сопротивляемостью – граница поля допуска.
Существо модели не изменится, если понятия «нагрузки» и «сопротивляемости» поменять местами. Графическое изображение нагрузки и сопротивляемости для этого случая показано на рис. 3.2, г.
5. Нагрузка – стационарный случайный процесс y(t), а сопротивляемость σ0 – случайная величина, не зависящая от времени. Этот случай является типичным для моделей расчета надежности механических конструкций, когда предельное состояние объекта проявляется в его «разрушении». Неопределенность значения нагрузки, приводящей объект к предельному состоянию - характерная черта технических объектов, измерение сопротивляемости которых сопряжено с их разрушением. Графическая модель зависимости нагрузки и сопротивляемости от времени показана на рис. 3.2, д.
6. Нагрузка - стационарный случайный процесс y(t), сопротивляемость – также стационарный случайный процесс σ0(t). Сопротивляемость в процессе работы (во времени) под воздействием переменных во времени факторов приобретает случайные, но обратимые изменения.
К такому случаю можно отнести изменение прочности обшивки самолета при небольших изменениях температуры, не приводящих к пластическим деформациям и усталостному разрушению. Графическая модель отказа приведена на рис. 3.2, е.
Теперь рассмотрим возможные модели отказов с учетом старения свойств объектов, т. е. с учетом необратимых изменений их сопротивляемости.
1. Нагрузка – случайная величина, не зависящая от времени, заданная плотностью распределения φ(у), а сопротивляемость σ0(t) – неслучайная функция времени. Величина изменения сопротивляемости обусловлена величиной действующей нагрузки и длительностью работы объекта. Зависимость сопротивляемости объекта от времени – это медленный процесс накопления необратимых изменений. Поэтому изменение сопротивляемости нередко представляет собой монотонно убывающую функцию времени.
Пусть σ0(t) – неслучайная монотонно убывающая функция времени, характеризующая предельные (допустимые) нагрузки (по условиям обеспечения прочности, т. е. неразрушимости объекта). Случайная величина y(t)=у0, являющаяся характеристикой, действующей на объект нагрузки, не зависит от времени. Условие отказа σ0(t)<y0.
Возможность появления отказа (разрушения) является функцией времени, зависящей от скорости «старения» объекта и характера функции распределения нагрузки (рис. 3.3, а).
2. Нагрузка – случайная величина y0, не зависящая от времени, а сопротивляемость σ0(t) – случайный сингулярный процесс («равномерная» функция старения) (рис. 3.3, б).
Иногда их называют функциями, зависящими от случайных параметров, или полуслучайными функциями: σ0(t)= σ(t, a, b). Рассматриваемый в этом случае процесс старения описывается линейной зависимостью сопротивляемости от времени. Скорость старения сопротивляемости не зависит ни от величины сопротивляемости, ни от времени.
Это более общий случай модели отказа, чем рассмотренная графическая модель на рис. 3.3, а. Условие отказа записывается так: σ(t)<y0.
Неопределенность времени безотказной работы в этом случае связана как с неопределенностью статической нагрузки, действующей на объект, так и со случайностью исходного значения сопротивляемости. Графическая модель этого случая взаимодействия, приводящего к отказу, показана на рис. 3.3, б.
3. Нагрузка – случайная величина y0, не зависящая от времени, а сопротивляемость – сингулярный случайны процесс старения веерного типа σ(t). Веерный сингулярный случайный процесс отличается от равномерного тем, что скорости старения отдельных его реализаций, будучи независимыми от време  ни, случайны и распределены по известному закону. Вследствие случайности скорости старения неопределенность величины сопротивляемости (ее рассеивание) зависит от времени, что и определяет веерный характер реализаций этого процесса. Условие отказа: σ(t)<y0.
ни, случайны и распределены по известному закону. Вследствие случайности скорости старения неопределенность величины сопротивляемости (ее рассеивание) зависит от времени, что и определяет веерный характер реализаций этого процесса. Условие отказа: σ(t)<y0.
Графическое изображение модели отказа для этого случая приведено на рис. 3.3, в.
| σ(t), y(t) |
| σ |
| S |
| t |
| σ(t), y(t) |
| S |
| t |
| φy(y) |
| φσ(σ) |
| σ(t), y(t) |
| t |
| y(t) |
| φσ(σ) |
| σ(t), y(t) |
| t |
| y(t) |
| φσ(σ) |
| σ(t), y(t) |
| t |
| y(t) |
| φσ(σ) |
| σ(t), y(t) |
| S |
| t |
| φy(y) |
| φσ(σ) |
а б
в г
д е
Рис. 3.3 Графические модели отказов с учетом старения сопротивляемости: а, б, в, - нагрузка - случайная величина; г, д, е – нагрузка - случайная функция времени
4. Нагрузка задана стационарным случайным процессом 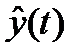 , а сопротивляемость
, а сопротивляемость 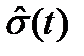 - сингулярным случайным процессом веерного типа.
- сингулярным случайным процессом веерного типа.
Такой пример характерен для объектов, сопротивляемость которых зависит от условий работы. Условие отказа записывается в форме неравенства: 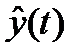 >
> 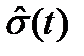 (рис. 3.3, г).
(рис. 3.3, г).
5. Нагрузка представляет собой стационарный случайный процесс 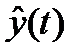 , а сопротивляемость
, а сопротивляемость 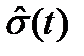 задана «равномерным» сингулярным нестационарным процессом (рис. 3.3, д)
задана «равномерным» сингулярным нестационарным процессом (рис. 3.3, д)
Это типичная для механических объектов модель отказа, отображающая взаимодействие объекта, подверженного «старению», с внешней средой. Формы функций старения 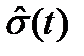 могут быть различными – линейными и нелинейными. Смысловое содержание этой модели таково: отказ наступает тогда, когда случайная величина сопротивляемости, являющейся функцией времени, превышена нагрузкой, являющейся также случайной функцией времени с неизменными вероятными характеристиками.
могут быть различными – линейными и нелинейными. Смысловое содержание этой модели таково: отказ наступает тогда, когда случайная величина сопротивляемости, являющейся функцией времени, превышена нагрузкой, являющейся также случайной функцией времени с неизменными вероятными характеристиками.
Условие отказа в этом случае выражают двухместным дважды неопределенным предикатом: 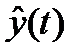 >
> 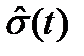 .
.
6. Наиболее общей формой модели взаимодействия объекта с окружающей средой является модель, отражающая зависимость характера реализаций сопротивляемости как от ее начального значения, так и от изменяющейся во времени скорости старения. Одна из возможных форм такого взаимодействия приведена на рис. 3.3, е. В данном случае рассматривается модель прогрессивно возрастающей во времени скорости старения объекта. Эта модель характерна для работы объектов в сильно агрессивных средах. Возможен и другой вариант этой модели, когда образующие окисные пленки снижают (тормозят) скорость старения сопротивляемости. Условие отказа в этом случае также записывается в форме двухместного дважды неопределенного предиката: 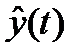 >
> 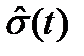 .
.
Случай, когда нагрузка и сопротивляемость нестационарные, случайные функции времени, не представляет принципиальных трудностей для описания самих факторов, приводящих к отказу, однако построение математической модели отказа при этом усложняется.
Дата добавления: 2015-03-14; просмотров: 1457;
