Теория восстановления и экономические критерии эксплуатации
Под восстановлением подразумевается процесс возвращения технической системы в функциональное состояние. Теория восстановления связана с простейшей моделью ремонта, когда после каждого отказа система приводится в исправное состояние за пренебрежимо малый отрезок времени. Несмотря на это, полученные при такой постановке выводы и вычислительные методы имеют большое практическое значение для планирования ремонтов.
В предыдущем разделе было показано, что максимизация функции готовности достигается посредством минимизации функции удельных затрат на эксплуатацию. Получение технического результата посредством регулирования экономических показателей (а не наоборот) выглядит несколько необычно. Однако, такое возможно, поскольку обе функции имеют одинаковую структуру и, следовательно, эквивалентные оптимизационные задачи.
В теории восстановления доказано, что с возрастанием времени эксплуатации происходит [2]:
1) монотонное возрастание среднего числа аварийных восстановлений Ih(τ)=1/ τh ,
2) монотонное убывание среднего числа профилактик Ip(τ)=1/ τp .
При этом τh и τp- соответственно, математическое ожидание времени между двумя аварийными восстановлениями и профилактическими. Удельное (на единицу времени) число ремонтов складывается из двух слагаемых: I (τ)= Ih(τ)+ Iр(τ).
Обозначим через ch и cp- средние, соответственно, аварийные и профилактические затраты на восстановление. Если интервал восстановления равен τ , то интенсивность эксплуатационных затрат будет:
R (τ)= ch Ih(τ)+ cp Ih(τ).
Из указанных положений следуют два вывода.
1. Поскольку функция интенсивности эксплуатационных затрат имеет ниспадающую и возрастающую ветвь, то ее график имеет вогнутую форму с наличием минимума. Соответствующий ему интервал восстановления (межремонтный период) τ* является оптимальным.
2.Функция коэффициента готовности КГ(τ) монотонно возрастает при убывании τ , поэтому для его (КГ) поддерживания на наибольшем уровне выгодно производить профилактики возможно чаще. Однако при этом возрастают затраты на восстановление, что препятствует значительному снижению времени τp.
Таким образом, оптимальный интервал восстановления τ* является решением уравнения dR/dτ=0. Его вид обусловлен типом отказов и альтернативными стратегиями восстановления.
Привнезапных отказах распространена стратегия строго периодического восстановления. Система восстанавливается после отказа (аварийно). Если она отработала без отказов заданный интервал времени, то производится профилактическая замена (рис. 6.1). В этом случае величина τ* определится из выражения:

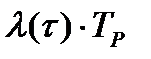
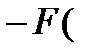
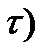
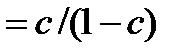 , (6.1)
, (6.1)
где λ(τ)- интенсивность отказов,
F(τ)-функция распределения наработки на отказ,
c=cp/ch. 

Например, для равномерно распределенной на интервале от 0 до Т наработки на отказ решение данного уравнения имеет вид (рис. 6.1):
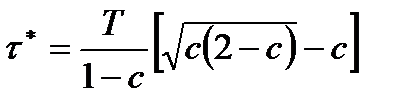 .
.  (6.2)
(6.2)
Отсюда видно, что оптимальный интервал профилактического восстановления резко уменьшается с ростом ущерба при авариях.
В общем случае решение уравнения (6.1) не выражается явно. Поэтому в специальной литературе имеются таблицы, номограммы для выбора оптимальных интервалов восстановления в зависимости от параметров распределения наработки и коэффициента затрат.
При постепенных отказах затраты за один цикл восстановления можно представить как сумму постоянных затрат С и переменных затрат А(τ) . Тогда по интенсивности последних a(t)=dA(t)/dt можно оценивать экономичное время эксплуатации.
В данной ситуации оптимальное время эксплуатации, соответствующее минимуму удельных затрат, является решением уравнения: 

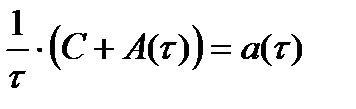 . (6.3)
. (6.3)
| 0 |
| τ |
| х |
| 2τ |
| х+τ |
| Профилактическая замена |
| Профилактическая замена |
| Аварийное восстановление |
Рис. 6.1 Строго периодическое восстановление
| 0 |
| 0,2 |
| 0,4 |
| 0,6 |
| 0,8 |
| Сp/Ch |
| 0,2 |
| 0,4 |
| 0,6 |
| 0,8 |
| τ*/Т |
Рис. 6.2 Оптимальные интервалы восстановления при строго
периодическом восстановлении
При линейной функции a(t)=at получаем:
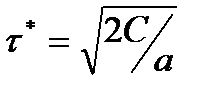 . (6.4)
. (6.4)
Соответствующая ей минимальная интенсивность эксплуатационных затрат будет [2]:
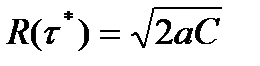 . (6.5)
. (6.5)
С помощью экономических критериев возможно также установить периодичность контролей технической системы. Дело в том, что зачастую неизвестно в исправном или неисправном состоянии находится оборудование. Это можно установить только после его контроля, диагностирования, ревизии, затраты на которые составляют величину с1. Возможна ситуация, когда параметрический отказ уже совершен, но система какое-то время работает с затратами на ее обслуживание (потерянной выгодой) равными с2, после чего отказ обнаруживается в момент контроля. Возникает задача оптимального с точки зрения общих затрат планирования проверок. Если приоритет отдается коэффициенту готовности системы, то возникает задача его максимизации при заданных затратах.
Обычно функция затрат с2 линейна во времени. Для экспоненциального распределения наработки F(t)=1-exp(t/T) достаточно точно можно определять оптимальный интервал контроля как [ 2]:
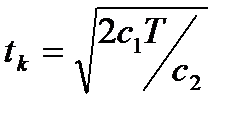 . (6.6)
. (6.6)
То есть периодичность контроля устанавливается меньше, чем среднеожидаемая наработка на отказ. Если же известно только математическое ожидание наработки Т, то периодичность контролей учащается:
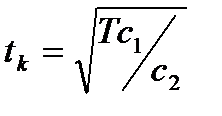 . (6.7)
. (6.7)
Дата добавления: 2015-03-14; просмотров: 1243;
