Теоретичні відомості. Математичний маятник являє собою матеріальну точку, підвішену на довгій та нерозтяжній нитці

Математичний маятник являє собою матеріальну точку, підвішену на довгій та нерозтяжній нитці. Деяким наближенням до математичного маятника буде пристрій, який складається з невеликої важкої кульки, підвішеної на довгій, тонкій, легкій, мало розтяжній нитці. Практично маса кульки повинна бути набагато більша за масу нитки, а розміри кульки набагато менші за довжину нитки.

Якщо кут відхилення маятника буде малим (до 10⁰), коливання будуть близькими до гармонічних і період коливань можна буде розрахувати за формулою (1), де Т – період коливань, l – довжина маятника, g – прискорення вільного падіння.

З формули (1) випливає, що прискорення вільного падіння 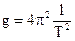. Але безпосереднє вимірювання довжини підвісу є досить складним завданням, тому що доводиться визначати центр мас кульки та положення точки підвісу. Тому роблять так: беруть маятник довільної довжини l₁ та визначають його період коливань Т₁: 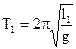(2). Потім укорочують його до довільної довжини l₂ і знову визначають його період коливань Т₂: 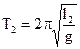(3). Виконавши математичні перетворення, отримаємо 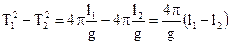. Тоді, прискорення вільного падіння g у місці проведення експерименту можна розрахувати за формулою: 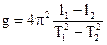. Таким чином, немає потреби вимірювати довжину маятника. Достатньо виміряти різницю довжин 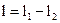за допомогою дзеркальної шкали, яка підвішена на стіні. Тоді, .

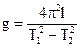Для вимірювання різниці довжин маятника l використовують повзунок, розташований на нитці, та дзеркальну шкалу, за якою вона буде дорівнювати різниці значень двох положень повзунка. Враховуючи, що 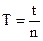, де t – час, за який маятник здійснив n коливань, отримаємо остаточно: 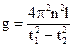(4).