Показательное распределение. Определение. Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины плотность которого имеет вид:

Определение. Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины плотность которого имеет вид:

где 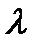− постоянная положительная величина.

Функция распределения показательного закона:

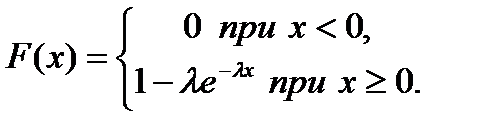
Вероятность попадания в интервал непрерывной случайной величины Х, распределенной по показательному закону, вычисляют по формуле:

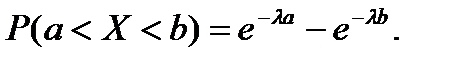(3.38)

Математическое ожидание, дисперсия и среднее квадратическое отклонение показательного закона распределения соответственно равны:

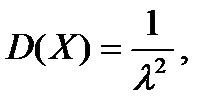
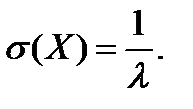(3.39)

Пример 3.54. Непрерывная случайная величина распределена по показательному закону с плотностью, равной:

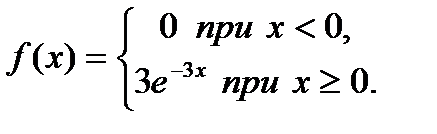
Найти вероятность того, что в результате испытаний значение непрерывной случайной величины 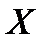попадет в интервал

По формуле (3.37) найдем:

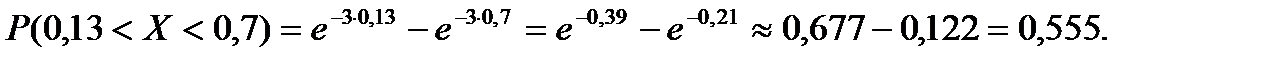
Контрольные вопросы

1. Сформулировать определение понятия дискретной случайной величины.

2. Что представляет собой закон распределения дискретной случайной величины?

3. Как вычисляются математическое ожидание, дисперсия и среднее квадратическое отклонение дискретной случайной величины?

4. Сформулировать определение понятия непрерывной случайной величины.

5. Сформулировать определение понятий плотности распределения вероятности и функции распределения непрерывной случайной величины.

6. Как вычисляются математическое ожидание, дисперсия и среднее квадратическое отклонение непрерывной случайной величины?

7. Как вычисляется вероятность попадания непрерывной случайной величины в заданный интервал?