Элементы математической статистики. В результате экономических, социологических, политологических и других исследований получают большие массивы статистических данных

В результате экономических, социологических, политологических и других исследований получают большие массивы статистических данных. Например, изучают распределение студентов первого курса г. Омска по росту (весу, состоянию здоровья, успеваемости и т. д.). Практически любой признак поддается непосредственному измерению либо может получить условную числовую характеристику. При этом некоторый признак элементов совокупности можно рассматривать как случайную величину, принимающую те или иные числовые значения с определенной вероятностью. В реальных исследованиях вероятность случайной величины оценивается с помощью ее относительной частоты при достаточно большом числе испытаний.

Основные задачи математической статистики

1. Определение методов сбора и группировки статистических сведений, полученных в результате экспериментов или наблюдений.

2. Разработка методов анализа статистических данных: оценка неизвестной вероятности, оценка зависимости случайной величины от других случайных величин и др.

Основные понятия математической статистики

Определение.Генеральной совокупностью называется совокупность всех элементов, обладающих интересующими исследователей признаками.

Определение. Выборочной совокупностью (выборкой) называется совокупность случайно отобранных элементов из генеральной совокупности.

Определение. Объемом совокупности называется количество элементов, содержащихся в этой совокупности.Например, если из 2000 изделий отобрано для обследования случайным образом 100 изделий, то объем генеральной совокупности N = 2000, а объем выборки n = 100.

Определение.Выборка называется репрезентативной (представительной), если по ее данным можно достаточно уверенно судить об интересующем признаке генеральной совокупности. Пусть из генеральной совокупности извлечена выборка объема n, в которой значение x₁ некоторого исследуемого признака X (размер одежды, заработная плата и пр.) наблюдалось n₁ раз, значение x₂ − n₂ раз, … , значение x_k − n_k раз.

Определение.Значения x_i (i = 1, 2, 3, …, k)исследуемого признака X называются вариантами, а их последовательность, записанная в возрастающем порядке, − вариационным рядом.

Определение.Число n_i, показывающее сколько раз наблюдалось значение x_i некоторого признака X в исследуемой совокупности, называется частотой.

Определение.Отношение частоты значения x_i некоторого признака X в исследуемой совокупности к объему выборки n называется относительной частотой:

. (3.40)

Необходимо отметить, что всегда выполняются равенства:

(3.41)

(3.42)

Определение.Размах выборки (обозначается − разность между максимальным и минимальным значениями случайной величины, полученными при исследовании выборки или длина интервала, которому принадлежат все значения варианты выборки:

.

Определение.Мода(обозначается 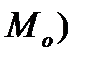– наиболее часто встречающееся значение случайной величины (исследуемого признака), полученное при исследовании выборки.

Определение.Ломаная, отрезки которой соединяют точки с координатами (х_i; n_i), где х_i – числовые значения исследуемого признака, а n_i – частота их появления в выборке, называется полигоном частот.

Наряду с полигоном частот можно построить полигон относительных частот, для этого по оси ординат необходимо откладывать относительные частоты .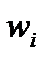

Определение.Гистограмма частот – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служатчастичные интервалы длины h, а высоты равны отношению (плотность частоты).

Площадь частичного i-го прямоугольника равна сумме частот, попавших в i-й интервал. Площадь гистограммы частот равна сумме всех частот, т. е. объему выборки n.

Определение.Гистограмма относительных частот – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служатчастичные интервалы длины h, а высоты равны отношению (плотность относительной частоты).

Площадь частичного i-го прямоугольника равна относительной частоте вариант, попавших в i-й интервал. Площадь гистограммы относительных частот равна единице.

Пример 3.55. Пусть исследуемый признак X – размер обуви мальчиков 9-х классов одной из школ имеет следующее распределение по частотам, представленное в виде таблицы 3.11.

Таблица 3.11

Распределение случайной величины по частотам

хi – размер обуви
ni− частота (количество учеников, имеющих определенный размер обуви)
− относительная частота

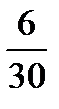
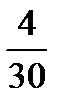
Размах и мода соответственно равны: 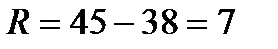и