Нормальное распределение. Определение. Нормальным называют распределение вероятностей непрерывной случайной величины Х, плотность которого имеет вид:
Определение. Нормальным называют распределение вероятностей непрерывной случайной величины Х, плотность которого имеет вид:
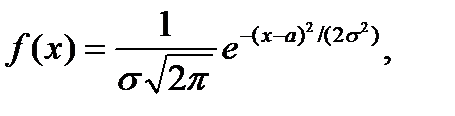
где 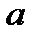 − математическое ожидание;
− математическое ожидание;
 − среднее квадратическое отклонение.
− среднее квадратическое отклонение.
Вероятность попадания значения случайной величины 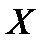 в интервал
в интервал 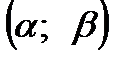 равна:
равна:
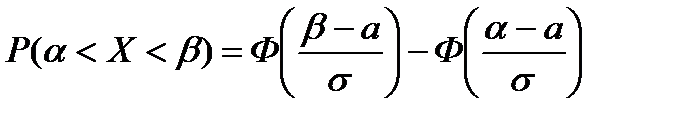 , (3.35)
, (3.35)
где  − функция Лапласа, значения которой представлены в приложении 2.
− функция Лапласа, значения которой представлены в приложении 2.
Вероятность того, что абсолютная величина отклонения меньше положительного числа 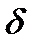 равна:
равна:
 (3.36)
(3.36)
В частности, при  справедливо равенство:
справедливо равенство:
 (3.37)
(3.37)
Пример 3.52. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины 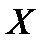 соответственно равны 10 и 2. Найти вероятность того, что случайная величина
соответственно равны 10 и 2. Найти вероятность того, что случайная величина 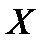 примет значение, заключенное в интервале
примет значение, заключенное в интервале  .
.
Воспользуемся формулой (3.30), учитывая, что 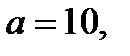
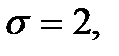

 получим:
получим:
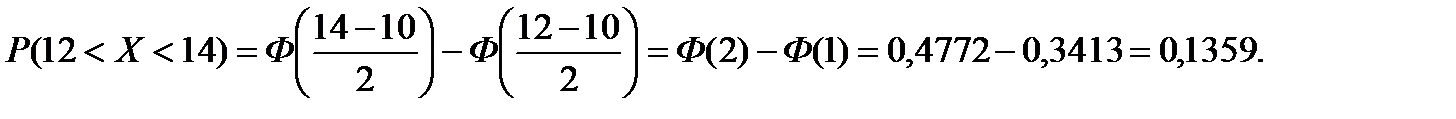
Значения  и
и  найдены из таблицы приложения 2.
найдены из таблицы приложения 2.
Пример 3.53. Случайные ошибки измерения 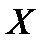 подчинены нормальному закону распределения со средним квадратическим отклонением
подчинены нормальному закону распределения со средним квадратическим отклонением  мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине
мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 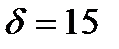 мм.
мм.
Математическое ожидание случайных ошибок равно нулю, поэтому, используя формулу (3.36), получим:
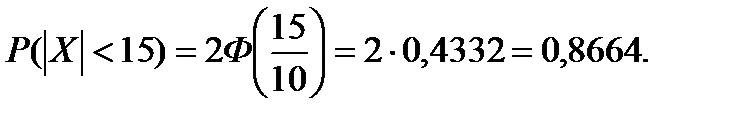
Дата добавления: 2014-12-14; просмотров: 920;
