В заданный интервал. Определение. Непрерывной случайной величиной Х, заданной на некотором интервале или ,называется такая случайная величина
Определение. Непрерывной случайной величиной Х, заданной на некотором интервале  или
или 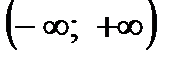 ,называется такая случайная величина, которая может принимать в результате серии испытаний любое значение из интервала
,называется такая случайная величина, которая может принимать в результате серии испытаний любое значение из интервала  или
или  .
.
Определение. Плотностью распределения вероятностей непрерывной случайной величины 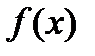 называется предел отношения вероятности попадания значения непрерывной случайной величины в интервал
называется предел отношения вероятности попадания значения непрерывной случайной величины в интервал 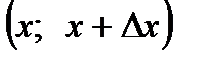 к
к 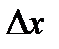 при
при 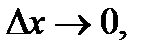 если такой предел существует:
если такой предел существует:
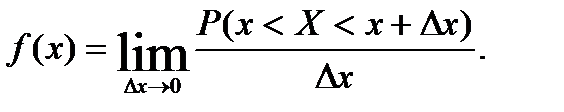
Свойства плотности распределения:
1. Плотность распределения неотрицательна, т. е. 
2. Несобственный интеграл от плотности распределения в пределах от 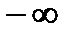 до
до 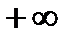 равен единице:
равен единице:
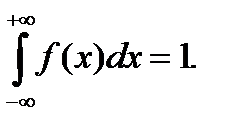
В частности, если все возможные значения непрерывной случайной величины 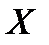 находятся в интервале
находятся в интервале  , то
, то 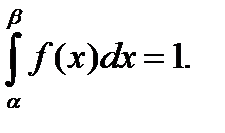
Определение. Функция распределения вероятностей 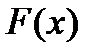 непрерывной случайной величины
непрерывной случайной величины 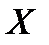 равна несобственному интегралу от плотности распределения
равна несобственному интегралу от плотности распределения  с переменным верхним пределом:
с переменным верхним пределом:
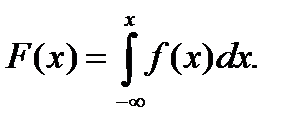 (3.29)
(3.29)
Исходя из выше изложенного, плотность вероятности можно определить как первую производную от функции распределения:
 (3.30)
(3.30)
Теорема. Пусть 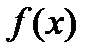 − плотность распределения вероятностей непрерывной случайной величины
− плотность распределения вероятностей непрерывной случайной величины 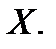 Тогдавероятность попадания значения случайной величины
Тогдавероятность попадания значения случайной величины 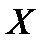 в интервал
в интервал 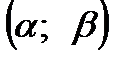 равна определенному интегралу от функции
равна определенному интегралу от функции 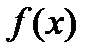 в пределах от
в пределах от 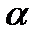 до
до 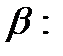
 (3.31)
(3.31)
Пример 3.47. Дана функция распределения непрерывной случайной величины Х:
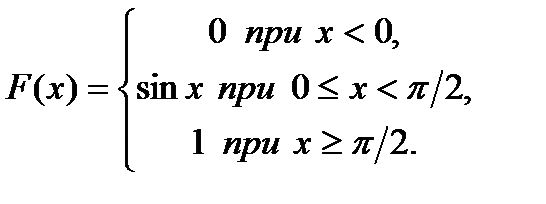
Найти плотность распределения 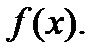
Плотность распределения равна первой производной от функции распределения:

Заметим, что при 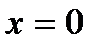 производная
производная 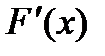 не существует.
не существует.
Пример 3.48. Дана плотность распределения непрерывной случайной величины 
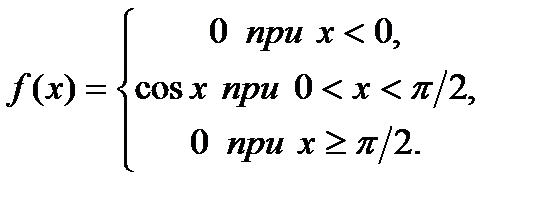
Найти функцию распределения 
Используем формулу 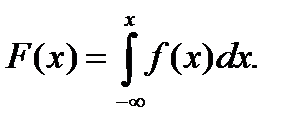
Если 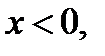 то
то 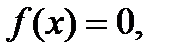 следовательно,
следовательно, 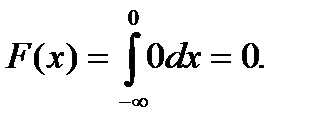
Если 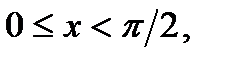 то
то 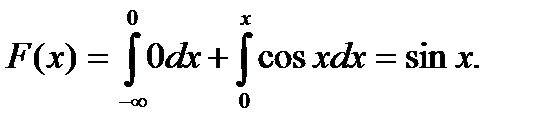
Если  то
то 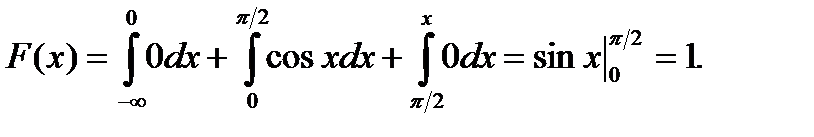
Таким образом, функция распределения 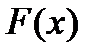 имеет вид:
имеет вид:
Пример 3.49. Дана плотность распределения непрерывной случайной величины Х:

Найти вероятность того, что непрерывная случайная величина 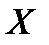 примет значение из интервала
примет значение из интервала 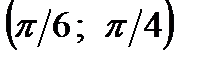 .
.
Воспользуемся формулой (3.30):
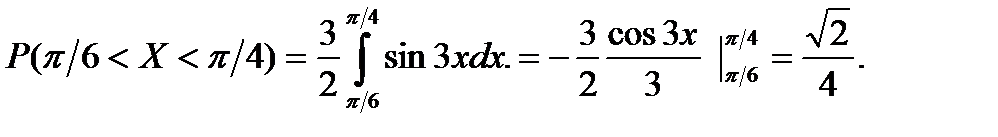
Дата добавления: 2014-12-14; просмотров: 1114;
