С постоянными коэффициентами. Составим характеристическое уравнение и решим его.
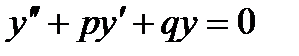 ,
,
где p, q 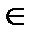 R.
R.
Решение.
Составим характеристическое уравнение 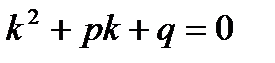 и решим его.
и решим его.
Возможны три случая:
1) k1,2 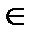 R, k1 ≠ k2 (дискриминант D > 0);
R, k1 ≠ k2 (дискриминант D > 0);
2) k1,2 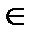 R, k1 = k2 = k (D = 0);
R, k1 = k2 = k (D = 0);
3) k1,2 = 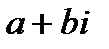
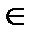 C (D < 0).
C (D < 0).
Каждому из этих случаев соответствует общее решение уравнения:
1) 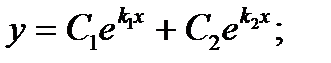
2) 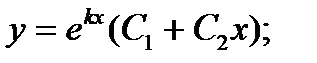
3) 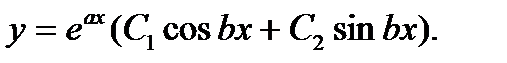
Пример 2.14.
Решить уравнения:
1) 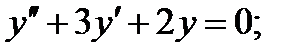
2) 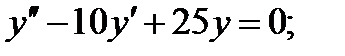
3) 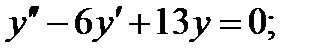
4) 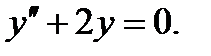
Решение.
1) 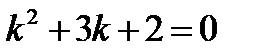
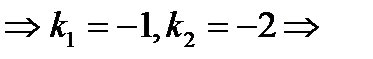 Ответ:
Ответ: 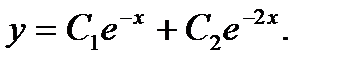
2) 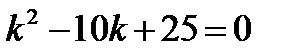
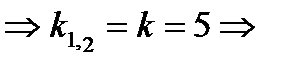 Ответ:
Ответ: 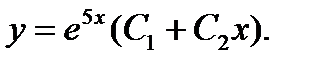
3) 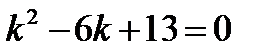
 Ответ:
Ответ: 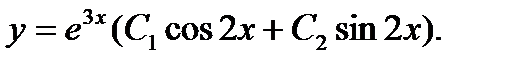
4) 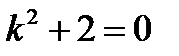
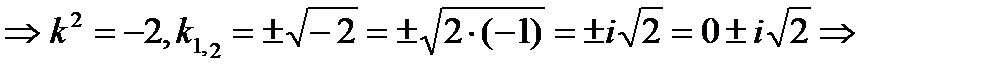
Ответ: 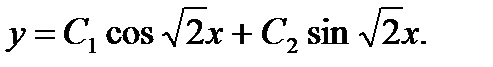
2.84. Решить уравнения:
1) 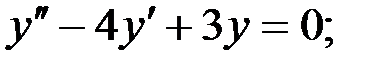 2)
2) 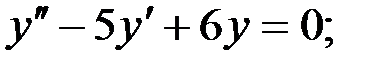 3)
3) 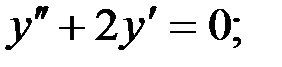
4) 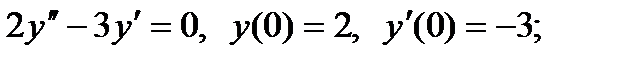 5)
5) 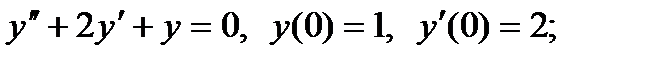
6) 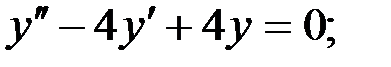 7)
7) 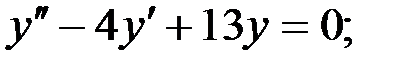 8)
8) 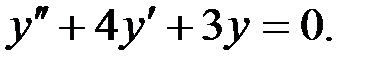
5. Уравнения вида y(n) = f(x)
Решение.
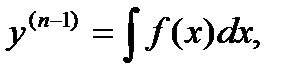
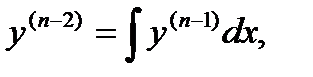 …,
…, 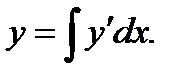
Пример 2.15.
Решить уравнение: 1.  2.
2. 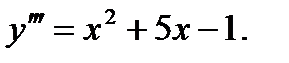
Решение.
1. 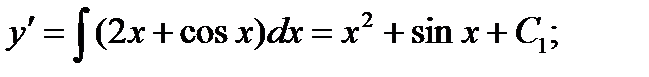
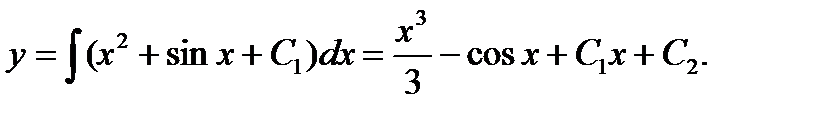
Ответ: 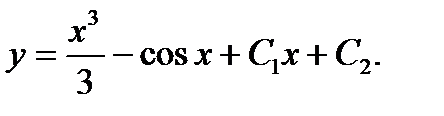
2. 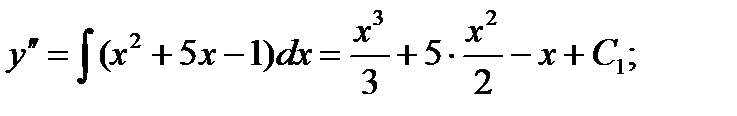
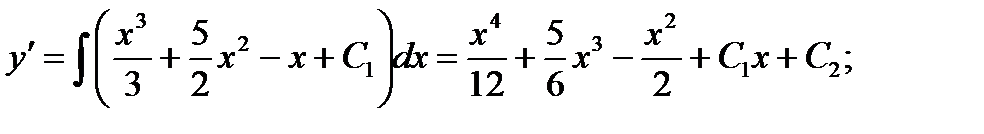
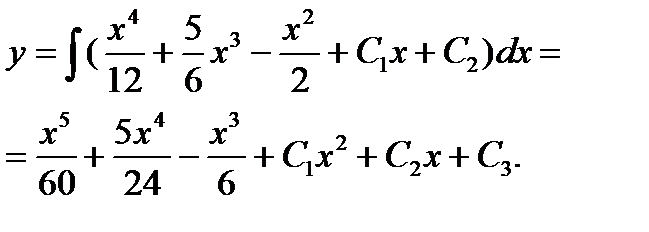
Ответ: 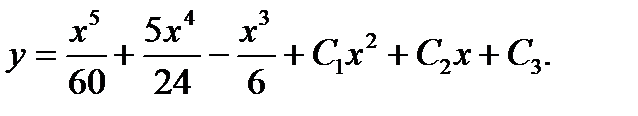
2.85. Установить вид частного решения неоднородного уравнения 2-го порядка с постоянными коэффициентами, если:
1) 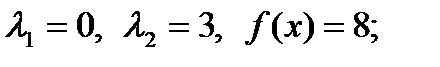 2)
2) 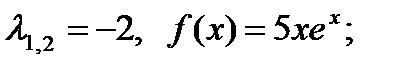
3) 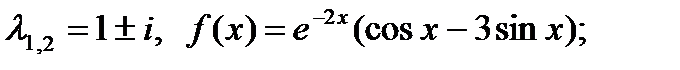
4) 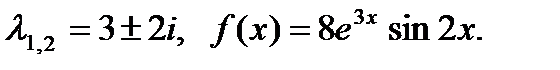
2.86. Решить уравнение или задачу Коши:
1) 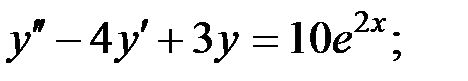 2)
2) 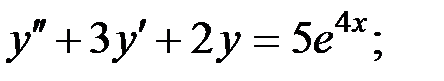
3) 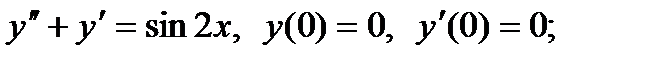
4) 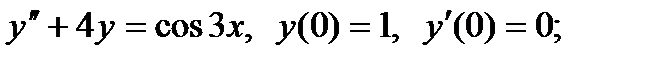
5) 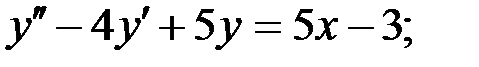
6) 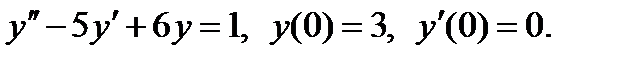
Дата добавления: 2014-12-14; просмотров: 821;
