Квадратные уравнения с комплексными коэффициентами.

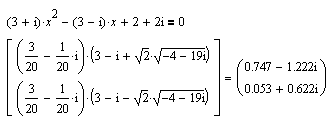
: При вводе уравнения с комплексными коэффициентами Сследует вводить для i: 1i; для -i: -1i; для 2i: 2i; ни в коем случае не вводить "*"! Как видим, MAthCAD неплохо справляется и с такими задачами.

Уравнения более высокого порядка.

Mathcad может решать уравнения вплоть до порядка 4 (даже символьно). Если возможно частичное разложение на множители, то разрешимы уравнения и более высокого порядка. Кубические уравнения.

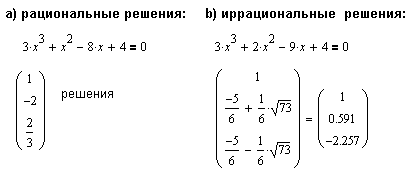
Уравнение седьмого порядка.

Иррациональное уравнения (уравнения с радикалами).

Корни (радикалы) могут вычисляться в MathCAD либо при помощи знака корня (клавиши [Ctrl+\]), либо как степени (клавиша [^] с дробными показателями. Знак квадратного корня вводится нажатием клавиши [\]. Знак корня и квадратный корень можно найти на панели Calculator (Калькулятор). Последовательность действий при решении уравнений с радикалами та же, что и при решении рассмотренных ранее уравнений.

С точки зрения теории, между решениями уравнений с радикалами и решением алгебраических уравнений имеется два важных различия, по крайней мере, при нахождении действительных решений.

• Радикалы определены не везде в действительной области. Это обстоятельство приводит к необходимости находить область определени, прежде чем решать само уравнение. Данная проблема справедливо игнорируется MathCAD, поскольку он не может знать, во множестве каких чисел (действительных или комплексных) вы намерены решать уравнение. Выход: вы можете самостоятельно найти область определения, воспользовавшись при этом возможностями MathCAD, связанными с решениями неравенств.
• Вторая проблема, возникающая при решении уравнений с радикалами, имеет принципиальный характер. Функция x² (как и любая другая функция с четным показателем) на является инъективной (проблема главных значений). В связи с этим возведение в квадрат обеих частей уравнения, содержащего квадратные корни, не является эквивалентным преобразованием. Как всегда, при применении к обеим частям уравнения не инъективного преобразования увеличивается множество решений. В результате в него могут войти "фиктивные" решения. Как ни удивительно, MAthCAD сам производит проверку решений на "фиктивность".

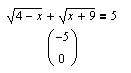
Классический случай решения уравнения с радикалами.

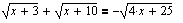
Mathcad распознает "фиктивные" решения (которые могут возникнуть в результате неэквивалентного преобразования "возведение в квадрат") и выдает верное сообщение: Решение не найдено. L = { }

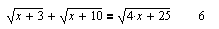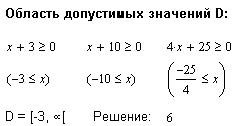
В приведенных примерах демонстрируется способность MathCAD находить область определения иррационального уравнения путем решения неравенств.

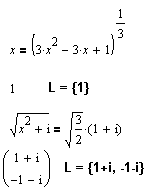
Уравнения с радикалами третьей степени, как и уравнения с комплексными коэффициентами, не представляют для MathCAD никакой сложности.

Уравнения с параметрами.
При решении уравнений с параметрами MathCAD ведет себя по-разному, в зависимости от того, каким образом производятся символьные вычисления - с помощью символьного знака равенства или команд меню Symbolics.

В данном примере использование палитры символьных преобразований позволяет решить уравнение (solve) и упрстить результат (simplify)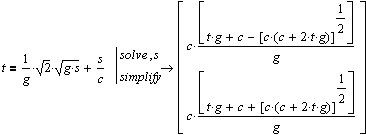
Экспоненциальные и логарифмические уравнения.

Определение: Уравнение, в котором независимая переменная входит в аргумент хотя бы одной экспоненциальной (логарифмической) функции, называется экспоненциальным (логарифмическим) уравнением.

Способ решения с помощью Mathcad такой же, как и для других типов уравнений.

Экспоненциальные уравнения во множестве действительных чисел не создают дополнительных сложностей в том смысле, что их область определения совпадает со множеством действительных чисел, а логарифмирование представляет собой инъективное отображение.

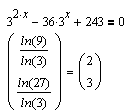
Если при решении экспоненциального уравнения возникают проблемы,их,как правило,можно устранить посредством вспомогательного логарифмирования. В крайнем случае можно обратиться к численным методам (См. Решение нелинейных уравнений и систем).

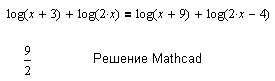
Значительно больше сложностей возникает при решении логарифмических уравнений. Область определения этих уравнений, если рассматривать их во множестве действительных чисел, как правило, не совпадает с действительной числовой прямой. MathCAD рассматривает логарифмические уравнения в комплексной области, т.е. не учитывая область определения.

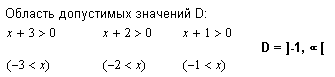
В данном примере показано, что MathCAD иногда находит решения (и даже действительные) там, где их быть не может (проблемы с комплексным логарифмом). Но нахождение области определения позволяет придти к верному решению.

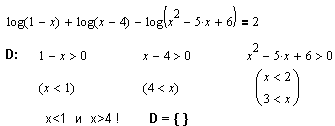
Насколько полезным может быть предварительное нахождение области определения, показывает следующий пример. Область определения пустое множество, следовательно,множество решений L={}.

Тригонометрические уравнения.

Сложность решения уравнений, содержащих тригонометрические функции, состоит прежде всего в том, что функций, обратных к тригонометрическим, не существует, а существуют лишь бесконечно многозначные обратные отображения. Поэтому прихдится мириться с тем, что любое вычислительное средство сможет найти только главное значение обратного выражения. Чтобы получить множество решений, необходимо самостоятельно воссоздать побочные значения обратного отображения.

Для тангенса (и котангенса) этого главного значения достаточно посредством периодического продолжения atan(x)+kp, где k - целое представить все решения. При решении уравнений с тангенсами и котангенсами возникает также вполне разрешимая проблема, связанная с тем, что данные функции определены не во всех точках числовой прямой.

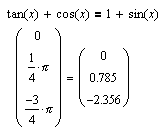
Данный пример показывает, что вышеуказанное ограничение не играет особой роли при решении уравнений с помощью MathCAD. Поскольку синус и косинус определены для всех значений аргумента, вопрос об области определения при решении уравнений, содержащих только эти тригонометрические функции, как правило, отпадает.

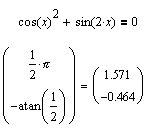
< Вместо этого возникает другая сложность: обратные функции asin(x) и acos(x), значениями которых являютмя главные значения обратных отображений, не дают всех решений в рамках одного периода (2p).

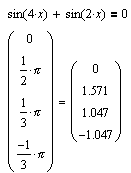
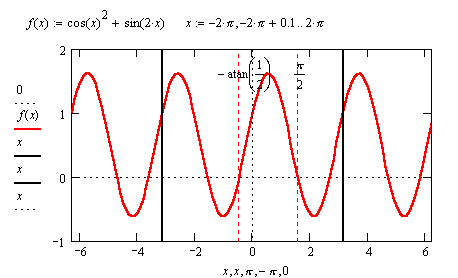
Поскольку остается неясным, какое именно из значений обратного отображения MathCAD рассматривает в качестве главного при решении уравнений, оказывается сложно получить еще одно значение, отстоящее от главного менее чем на период; тем самым задача была бы решена с точностью до периода. В подобных ситуациях на выручку приходит построение графиков.

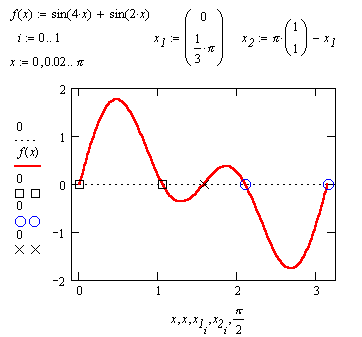
Данный пример демонстрирует пределы возможности MathCAD. Решение в лоб не дает никаких результатов.

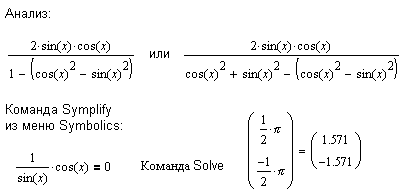
<	Проведя дополнительные преобразования, нам все-таки удается найти решение.

Неравенства.

MathCAD обладает достаточно мощными возможностями для решения неравенств. Эти возможности уже использовались нами ренее для нахождения области определения уравнений, содержащих функции, определенные не во всех точках числовой прямой.

Неравенства, как и уравнения, можно решать либо с использованием символьного знака равенства, либо, отметив переменную следм курсора, посредством выполнения команды Solve (Вычислить) подменю Variable (Переменные) меню Symbolics (Символы). В разных неравенствах могут быть использованы различные знаки неравенств.

Знаки "больше" и "меньше" могут вводиться непосредственно с клавиатуры. Все остальные знаки можно вводить при помощи панели Evaluation (Вычисления), либо сочетанием клавиш.

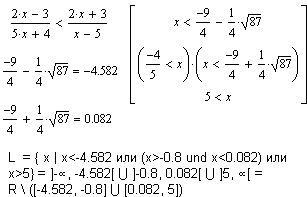
Линейные неравенства и неравенства с дробно-рациональными функциями не составляют сложности для MathCAD.

Неравенства с параметрами удобно анализировать с использованием знака символьного равенства, если значения параметра ограничены некоторыми условиями.

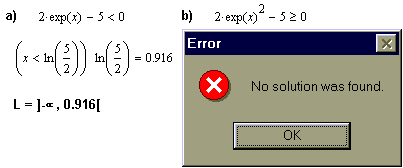
При решении неравенств, содержащих трансцендентные функции,возможности MathCAD ограничены.

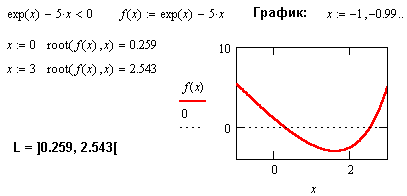
В данном примере MathCAD не может решить неравенство при использовании символьного процессора. На помощь приходят графики и функция численного решения уравнений root. Для работы этой функции необходимо задать начальное приближение для искомого решения.

Системы линейных уравнений.

Для численного решения линейных систем уравнений в MathCAD имеется специальная функция:

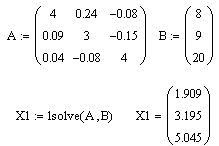
lsolv(A,B) Она решает систему линейных алгебраических уравнений вида А x X =B, выдавая решение - вектор X. А - матрица коэффициентов размерности nxn; В - вектор свободных членов размерности n ; X - вектор неизвестных пока решений.

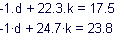
Эквивалентной для MathCAD формой представления систем линейных уравнений является матричная форма. Представленные таким образом системы можно решать как символьно, так и численно.

Хорошей альтернативой решению систем в матричной форме является так называемый solve block (Блок решения). Он удобен тем, что при его использовании уравнения записываются не в матричной, а в обычной форме, а также тем, что позволяет решать нелинейные уравнения и вводить ограничительные условия для определяемого решения. Блок решения применяется как для нахождения численного решения, так и для отыскания решеня в символьном виде.

Синтаксис Блока решения:

Given

Уравнения

Ограничительные условия

Find(v1,v2,...vn) - возвращает значение одной

или ряда переменных для точного решения

vi - переменные, которые надо найти.

Последовательность действий при численном решении:

Задаем начальные (стартовые) значения для искомых переменных. Заключаем уравнения в блок решения, начинающийся ключевым словом Given и заканчивающийся ключевым словом Find(v1,v2,...vn). Если после слова Find(v1,v2,...vn) ввести знак равенства [=], MathACD выдаст численное решение.

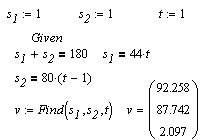
При символьном решении не надо вводить начальные значения, а после ключевого слова Find(v1,v2,...vn) вместо знака равенства следует ввести символьный знак равенства (при помощи комбинации [Ctrl+.] или соответствующей пиктограммы панели Evaluation).

Существует еще одно важное отличие между блоком решения и использованием матричных операций. Если определитель матрицы коэффициентов равен нулю, матричные методы оказываются непригодными. В таком случае система не имеет решений или разрешима неоднозначно. Если же применить блок решения, MathCAD распознает неоднозначность и выдает решение в параметрической форме.

Нелинейные уравнения и системы уравнений.

Многие уравнения, например трансцендентные, и системы из них не имеют аналитических решений. Однако они могут решаться численными методами с заданной погрешностью (не более значения, заданного системной переменной (TOL). Для простейших уравнений вида F(x)=0 решение находится с помощью функции