Розробка системи автоматичного керування з використанням лінійно-квадратичного П-регулятора з наглядачем стану

На відміну від підходів класичної теорії керування, що намагається скоротити кількість розглянутих зв'язків і керований змінних, підхід сучасної теорії керування настроєний, навпаки, на більшу деталізацію математичних моделей, що пов'язано з розвитком засобів обчислювальної техніки. Лінійно-квадратичний регулятор (англ. Linear quadratic regulator, LQR) – один із видів оптимальних регуляторів, що використовується для керування складними багатомірними й багатозв´язними об'єктами управління. Даний регулятор використовує метод подання динаміки систем у вигляді простору станів - системи лінійних ЗДР у формі Коші, записаних в матричній формі.

У безперервному часі критерій оптимальності лінійно-квадратичного регулятора може бути представлений у такий спосіб:

(23)

де: x – вектор змінних стану,

u – вектор керуючих впливів,

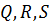- матриці вагових коефіцієнтів.

У класичній теорії керування зазвичай рекомендується критерій [9], що для систем у формі простору станів у безперервному часі може бути представлений у наступному вигляді:

(24)

Модифікуємо його, підставляючи значення похідної з рівняння системи, зведемо цей критерій до критерію J, підстановкою:

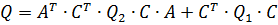
	(25)
	(26)
	(27)

Аналогічний критерій можна записати для системи в дискретному часі:

,

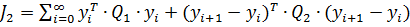(28)

який зводиться до критерію J у дискретному часі підстановкою:

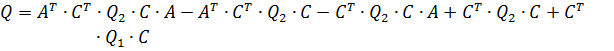
	(29)
	(30)
	(31)

Для перевірки придатності розробленої математичної моделі високого порядку для завдань синтезу автоматизованих систем керування проведемо синтез лінійно-квадратичного П-регулятора. Для цього створимо в Matlab програму.

Представимо модель у вигляді матриць передаточних функцій:

P=[yy1_opup_1s yy1_opup_2s yy1_opup_3s yy1_opup_4s yy1_opup_5s yy1_opup_6s;

yy2_opup_1s yy2_opup_2s yy2_opup_3s yy2_opup_4s yy2_opup_5s yy2_opup_6s;

yy3_opup_1s yy3_opup_2s yy3_opup_3s yy3_opup_4s yy3_opup_5s yy3_opup_6s;

yy4_opup_1s yy4_opup_2s yy4_opup_3s yy4_opup_4s yy4_opup_5s yy4_opup_6s;

yy5_opup_1s yy5_opup_2s yy5_opup_3s yy5_opup_4s yy5_opup_5s yy5_opup_6s;

yy6_opup_1s yy6_opup_2s yy6_opup_3s yy6_opup_4s yy6_opup_5s yy6_opup_6s];

Для перетворення передаточних функцій у простір станів використаємо функцію MatLab ss:

P_ss=s s(P);

Для перетворення математичної моделі у дискретний час використовується функція c2d. Функція c2d виконує дискретизацію безперервної моделі. Ця команда підтримує кілька видів квантування / відновлення: відновлення нульового порядку (ZOH - Zero-Order Hold), відновлення першого порядку (FOH - First-Order Hold), апроксимацію Тастіна без і з попередньою модифікацією частот, з узгодженням полюсів і нулів. Синтаксис цих команд (з ZOH за замовчуванням) такий:

sysd = c2d(sysc,Ts) % Ts - період квантування або вибірки в секундах

sysc = d2c(sysd)

Дискретна функція за методом ZOH Hd (z) виходить з безперервної функції H (s) за такою схемою

Рисунок 4.1 – Схема перетворення безперервної функції у дискретну за методом ZOH

Пристрій ZOH генерує безперервний вхідний сигнал u (t), утримуючи постійним значення кожної вибірки u [k] протягом одного періоду квантування, тобто

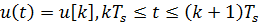
Сигнал u(t) потім подається на безперервну систему H(s) і вихідний сигнал y(t) квантується кожні T_S секунд, щоб отримати дискретний вихідний сигнал y[k].

Крок дискретності має бути обрано з урахуванням того, що процеси у замкненій системі будуть десь у 10 разів більш швидкими, ніж у об’єкті. Тобто знайти за формулою:

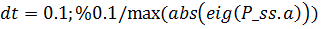
де: ,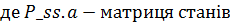

фунція mах(А) - повертає найбільший елемент, якщо А - вектор, або повертає вектор-рядок, що містить максимальні елементи кожного стовпця, якщо А - матриця, в багатовимірних масивах працює з першою не одиничної розмірності,

функція abs (X) - повертає абсолютну величину для кожного числового елемента вектора X,

функція eig (A) обчислює власні значення матриці A.

Перетворення у дискретний час:

де: P_ss -матриці станів,

P_ssd -матриці станів у дискретному часі.

Матриці параметрів регулятора розраховані за допомогою програми dlqr:

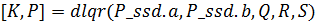
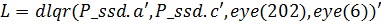
функція dlqr:

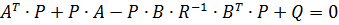
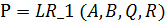
де Q,R,Q1,R1- вагові матриці.

Вагові матриці Q,R,Q1,R1 спочатку мають бути обрані одиничними (для зручності одиничну матрицю генерує програма eye). Після оцінки якості перехідного процесу матриці Q, R потрібно відкоригувати збільшивши відповідний елемент Q, якщо вихідна змінна має велике перерегулювання, і збільшивши R, якщо керуючий вплив перевищує обмеження.

На підставі побудованої математичної моделі високого порядку в пакеті Matlab проведемо математичне моделювання реакції замкнутої АСР із лінійно-квадратичним регулятором зі стандартним і модифікованим критерієм на збурення величиною -5% х.в.м. по всіх каналах ОУ (рис. 4.3).

Рисунок 4.3 - Модель замкнутої системи в Simulink

Перехідні процеси по збуренню:

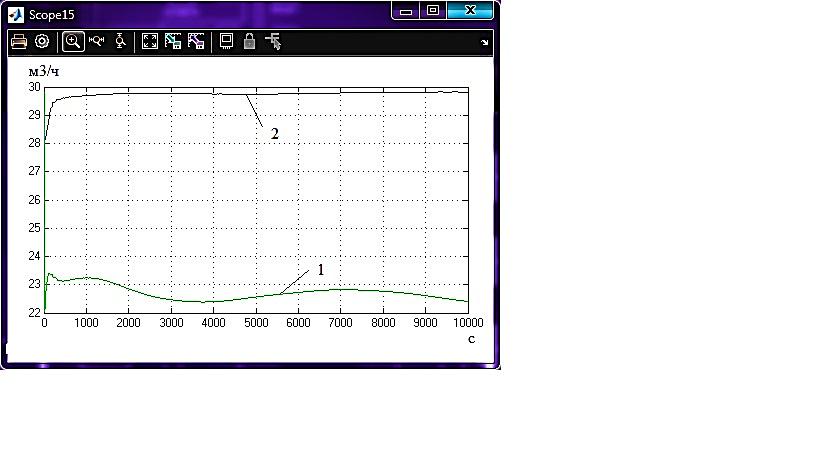
Рисунок 4.4 - Перехідний процес по першому каналу

Рисунок 4.5 - Перехідний процес по другому каналу

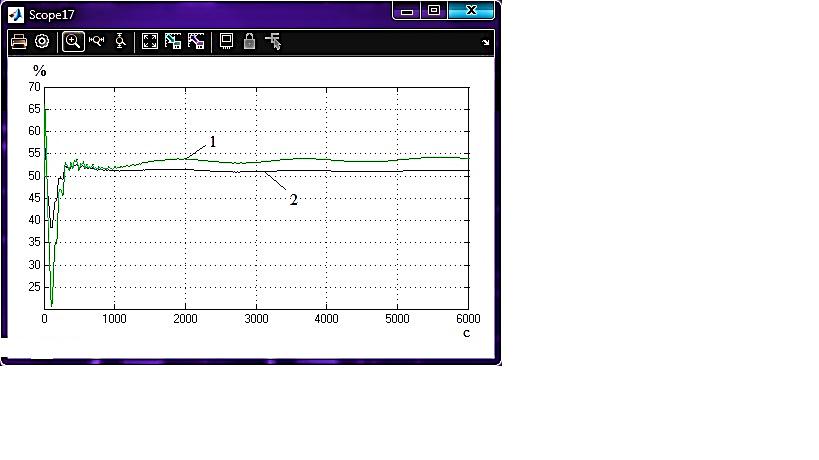
Рисунок 4.6 - Перехідний процес по третьому каналу

Рисунок 4.7 - Перехідний процес по четвертому каналу

Рисунок 4.8 - Перехідний процес по п'ятому каналу

Рисунок 4.9 - Перехідний процес по шостому каналу

Рисунок 2 – Переходные процессы АСР с линейно-квадратичным регуляторов при управлении по возмущению с использованием для синтеза регулятора стандартного (1) и модифицированного критерия оптимальности (2)

Как видно из графиков переходных процессов (рис.2), использование модифицированного критерия для синтеза линейно-квадратичного регулятора в сравнении со стандартным позволяет повысить качество системы регулирования, что особенно актуально для сложных технологических объектов управления, таких как атмосферная ректификационная колонна К-2. Для расхода газойля из стриппинга, при использовании модифицированного критерия оптимальности, время установления процесса – 2000с, для расхода дизеля из стриппинга – 8000с, для уровня керосина в ребойлере – 1000с, для температуры орошения – 1000с, для уровеня в конденсаторе – 750с, и для температуры флегмы – 6000с. Переходные процессы имеют значительно меньшую статическую ошибку, также уменьшилось время регулирования и величина перерегулирования.