Розробка експериментальної лінійної математичної моделі динаміки методом активного експерименту

Розробка математичної моделі може здійснюватися за допомогою можливостей HYSYS, але недоліком даного способу є його орієнтація скоріше на пасивний експеримент, ніж на активний, тому графіки перехідних процесів до сталих значень не доходять через неконтрольований інтервал зміни стрибка.

Тому доцільно використати наявну в HYSYS модель, доповнюючи її можливостями пакета Matlab. Для обміну інформацією програм мовою Matlab з HYSYS скористаємося бібліотекою для роботи з HYSYS за допомогою протоколу DDE. Разом з нею необхідно використати 3 функції (Додаток В?): ініціалізації (init_hysys.m), зміни параметра (setHysVar.m), одержання значення параметра (getHysVar.m).

В HYSYS задаємо параметри, що підлягають одержанню й передачі. Для цього створюється електронна таблиця (Spread Sheet) з параметрами каналів, що одержує автоматичне ім'я SPRDSHT-1.

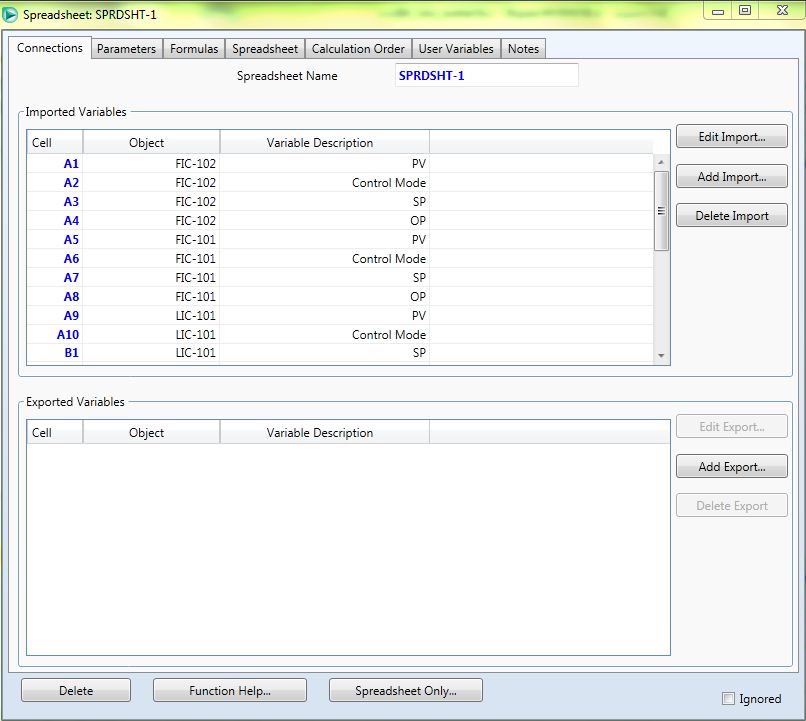
Рисунок 3.1 - Параметри, що підлягають одержанню й передачі

Наведена програма проводить активний експеримент й автоматично апроксимує передатні функції за допомогою функцій Identification Toolbox.

Активний експеримент виконується за планом:

1. Стабілізація параметрів за допомогою регуляторів

2. Провести стрибок величиною 10% по витраті газойля зі стріппінгу

3. Стабілізація параметрів за допомогою регуляторів

4. Провести стрибок величиною 10% по витраті дизеля зі стріппінгу

5. Стабілізація параметрів за допомогою регуляторів

6. Провести стрибок величиною 10% по витраті зрошення в колону

7. Стабілізація параметрів за допомогою регуляторів

8. Провести стрибок величиною 10% по рівню гасу в ребойлері

9. Стабілізація параметрів за допомогою регуляторів

10. Провести стрибок величиною 10% по температурі зрошення

11. Стабілізація параметрів за допомогою регуляторів

12. Провести стрибок величиною 10% по температурі флегми

13. Стабілізація параметрів за допомогою регуляторів

14. Апроксимація передаточних функцій за допомогою Identification Toolbox.

У результаті виконання програми одержимо графіки розгінних характеристик.

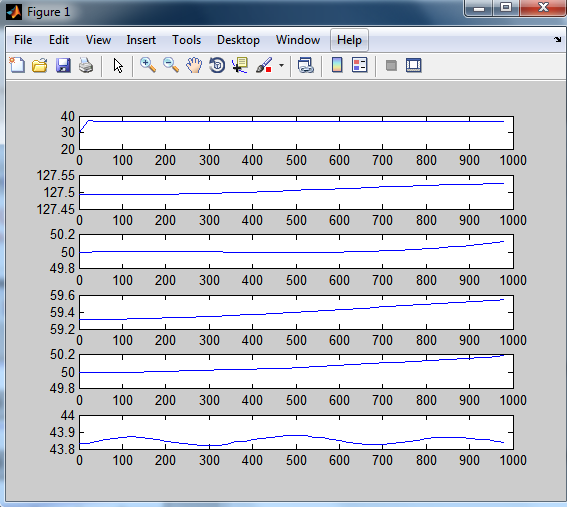
Рисунок 3.2 – Реакція каналів на стрибок 10% по витраті атмосферного газойлю

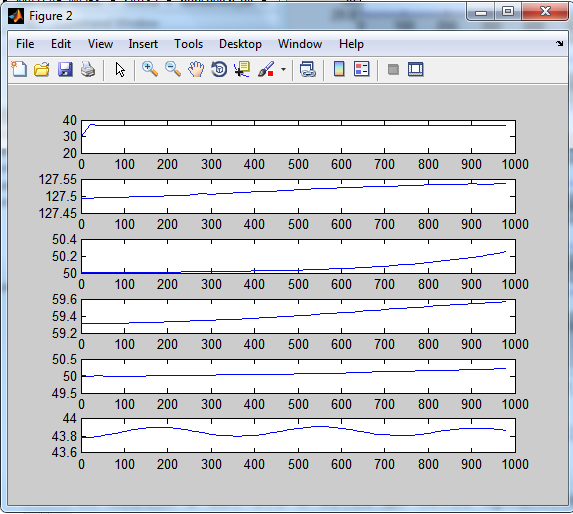
Рисунок 3.3 – Реакція каналів на стрибок 10% по витраті 10% по витраті дизеля

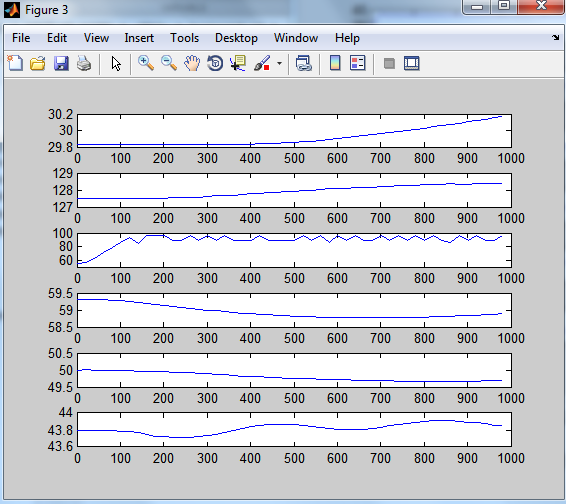
Рисунок 3.4 – Реакція каналів на стрибок 10% по витраті зрошення в колону

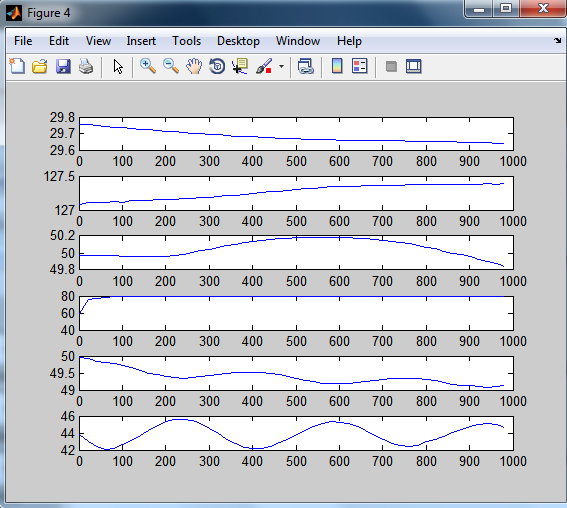
Рисунок 3.5 – Реакція каналів на стрибок 10% по витраті в ребойлері

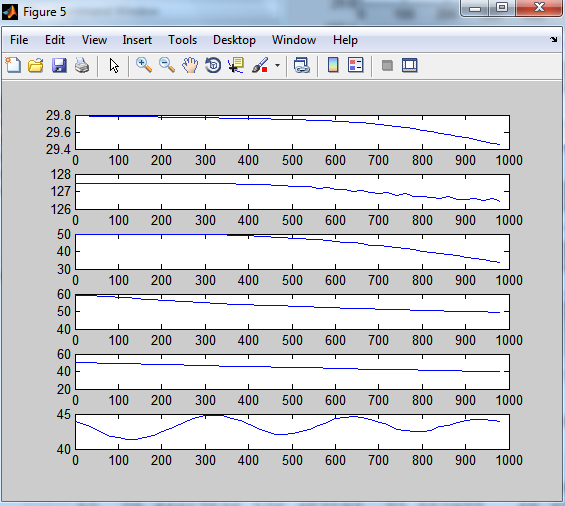
Рисунок 3.6 – Реакція каналів на стрибок 10% по витраті в конденсаторі

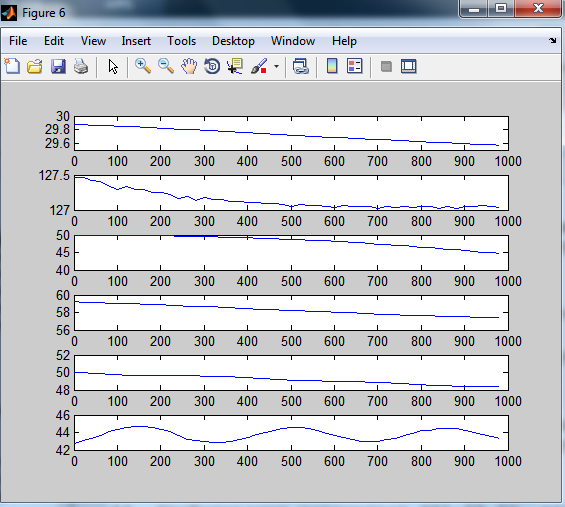
Рисунок 3.7 – Реакція каналів на стрибок 10% по витраті рефлюксу

Апроксимація передатних функцій за допомогою функцій Identification Toolbox дає наступні результати:

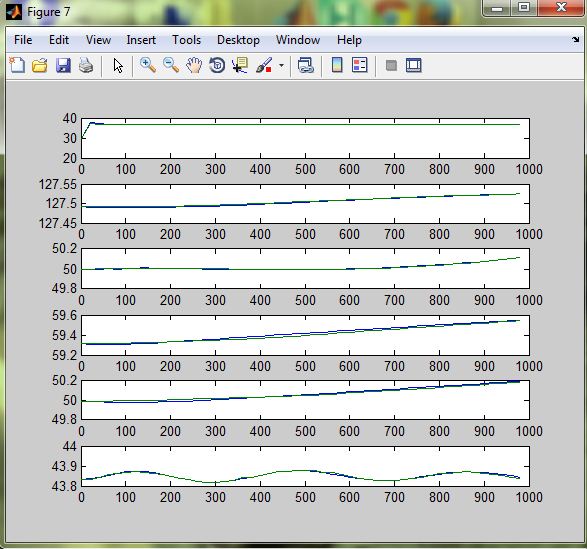
Рисунок 3.8 - Розгінні характеристики при u1=+10%

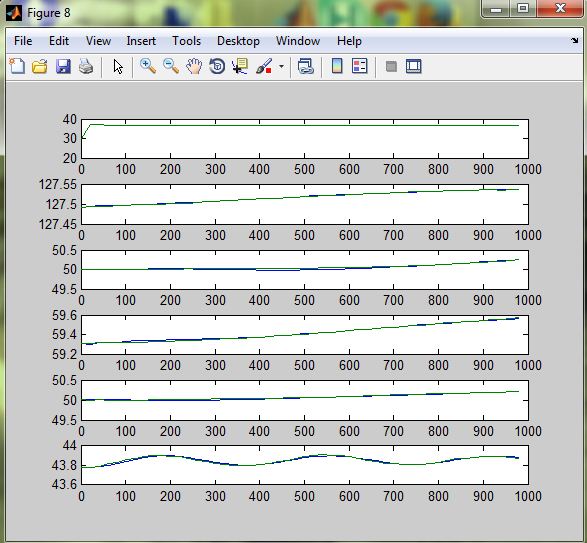
Рисунок 3.9 - Розгінні характеристики при u2=+10%

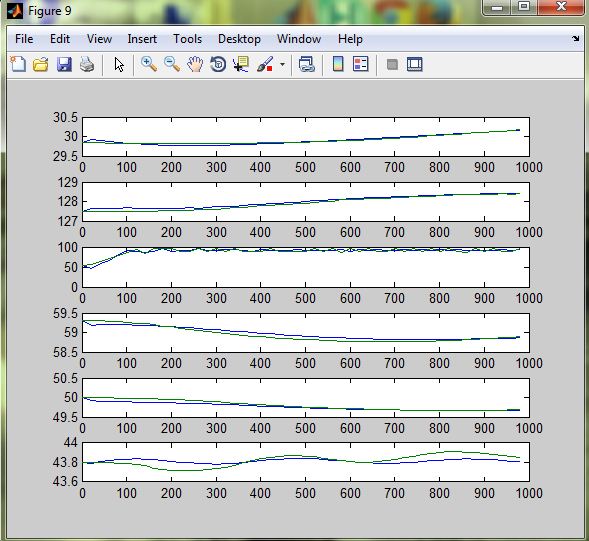
Рисунок 3.10 - Розгінні характеристики при u3=+10%

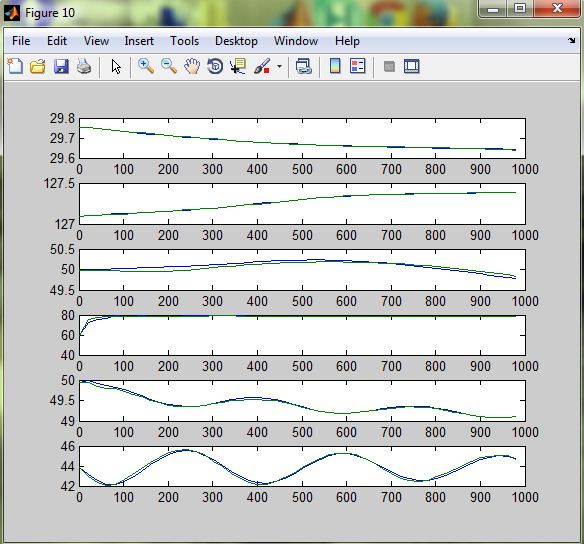
Рисунок 3.11 - Розгінні характеристики при u4=+10%

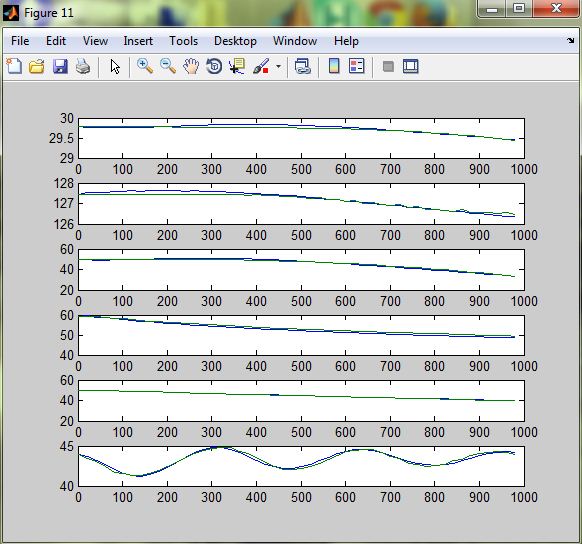
Рисунок 3.12 - Розгінні характеристики при u5=+10%

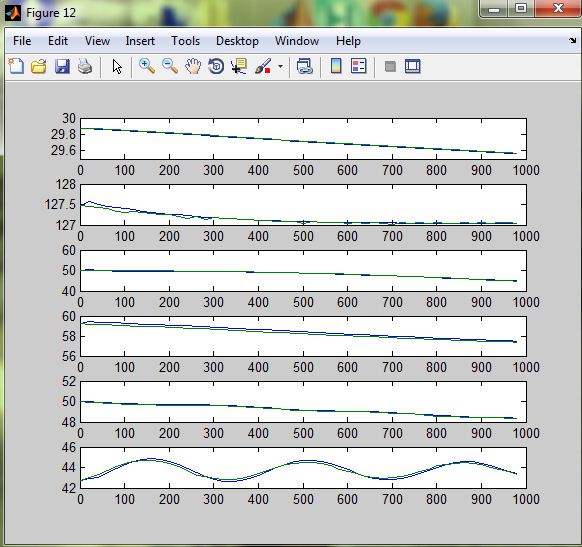
Рисунок 3.13 - Розгінні характеристики при u6=+10%

Розгінні характеристики апроксимованих передаточних функцій високого порядку майже повністю збігаються з експериментальними розгінними характеристикам, тому можна вважати апроксимовану математичну модель адекватною. Отримані передаточні функції наведені у додатку Б.