Вибір моделі об'єкта дослідження.

Планування експерименту базується на кібернетичних поданнях про об'єкт досліджень. У зв'язку із цим, при новому підході до проведення експерименту в якості найбільше підходящої моделі об'єкта досліджень рекомендується вибирати так званий чорний ящик (Рис. 5.1).

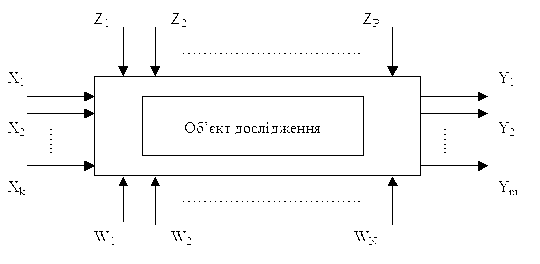
Рис.5.1. Модель об'єкта досліджень

Принципи побудови такої моделі звичайно відповідають апріорним поданням експериментатора про об'єкт дослідженні при рішенні в умовах неповного знання механізму явищ складних багатофакторних задач.

До числа вхідних параметрів об'єкта дослідження відносять керуючі, контрольовані й параметри, що обурюють. Керуючі параметри (або фактори) Х₁, Х₂, ... , Х_k − основні, на них можна впливати з метою зміни стану об'єкта (зміни вихідних параметрів об'єкта).

Контрольовані параметри Z₁, Z₂, ... , Z_Р вимірюють у процесі дослідження, їх не змінюють цілеспрямовано (звичайно можливість впливу на них відсутній).

Параметри, що збурюють (_W1, _W2…,W_N) − неконтрольовані, вони недоступні для виміру, їхні значення змінюються в часі випадковим образом.

Застосовувані моделі в загальному виді мають форму рівнянь виду:

.

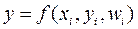де f − функція, що задає співвідношення між X_i, Z_i і W_i.

Метою експерименту є вивчення залежності між вихідними параметрами й факторами, тому модель об'єкта дослідження шукається у вигляді рівняння:

.

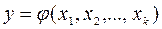Звичайно вище наведена залежність шукається у вигляді поліномінального рівняння, тобто:

.

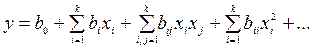По величині коефіцієнтів полінома (коефіцієнтів регресії) судять про ефекти або про ступінь впливу відповідних факторів на величину Y.

Ступінь полінома підвищують у кілька послідовних етапів, після того, як доведена необхідність цього на попередніх стадіях дослідження.

На першому етапі модель об'єкта шукається у вигляді полінома першого порядку, що містить вільний член, члени з лінійними ефектами й члени з ефектами взаємодії всіх порядків.

Так, у даній курсовій роботі для k = 4 така модель буде мати вигляд:

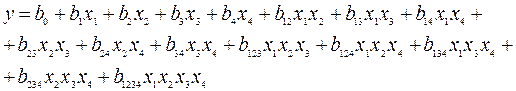
Число лінійних коефіцієнтів рівняння регресії знайти легко: воно дорівнює числу факторів, що враховують відповідною матрицею ПФЭ.