График гиперболы
Опять же вспоминаем тривиальную «школьную» гиперболу 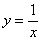 .
.
Выполним чертеж:

Основные свойства функции 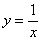 :
:
Область определения: 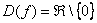 .
.
Область значений: 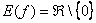 .
.
Запись 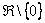 обозначает: «любое действительное число, исключая ноль»
обозначает: «любое действительное число, исключая ноль»
В точке  функция терпит бесконечный разрыв. Или с помощью одностороннихпределов:
функция терпит бесконечный разрыв. Или с помощью одностороннихпределов: 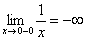 ,
, 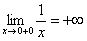 . Немного поговорим об односторонних пределах. Запись
. Немного поговорим об односторонних пределах. Запись 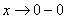 обозначает, что мы бесконечно близко приближаемся по оси
обозначает, что мы бесконечно близко приближаемся по оси 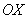 к нулю слева. Как при этом ведёт себя график? Он уходит вниз на минус бесконечность, бесконечно близко приближаясь к оси
к нулю слева. Как при этом ведёт себя график? Он уходит вниз на минус бесконечность, бесконечно близко приближаясь к оси  . Именно этот факт и записывается пределом
. Именно этот факт и записывается пределом 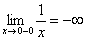 . Аналогично, запись
. Аналогично, запись 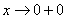 обозначает, что мы бесконечно близко приближаемся по оси
обозначает, что мы бесконечно близко приближаемся по оси 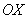 к нулю справа. При этом ветвь гиперболы уходит вверх на плюс бесконечность,бесконечно близко приближаясь к оси
к нулю справа. При этом ветвь гиперболы уходит вверх на плюс бесконечность,бесконечно близко приближаясь к оси  . Или коротко:
. Или коротко: 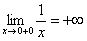 .
.
Такая прямая (к которой бесконечно близко приближается график какой-либо функции) называется асимптотой.
В данном случае ось  является вертикальной асимптотой для графика гиперболы при
является вертикальной асимптотой для графика гиперболы при 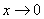 .
.
Дата добавления: 2014-11-29; просмотров: 1593;
