Релятивистский импульс

Ранее была установлена инвариантность законов Ньютона, следовательно, и вытекающего из них закона сохранения импульса относительно преобразований Галилея. Однако инвариантность этих законов по отношению к преобразованиям Лоренца не соблюдается.

В СТО найдено новое выражение для импульса частицы, такое что 1) закон сохранения импульса остается инвариантным по отношению к преобразованиям Лоренца как при больших, так и при малых скоростях и 2) при 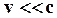остается справедливым ньютоновское определение импульса.

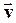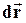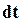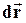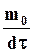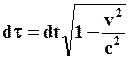Рассмотрим частицу, движущуюся со скоростью относительно неподвижной инерциальной системы отсчета; - вектор перемещения частицы за время . Умножим на постоянную величину , где - собственное время частицы, 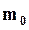- некоторая постоянная:

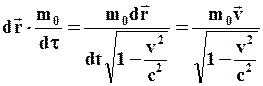(82)

Допустим, что 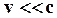, так что 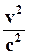можно пренебречь, и возьмем в качестве 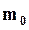массу частицы, как она определяется в классической механике. При этих условиях 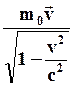перейдет в 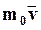. В классической механике этот вектор, как известно, называют импульсом частицы. Поэтому в релятивистской механике естественно импульс определить выражением:

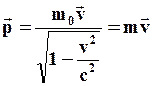(83)

Величина

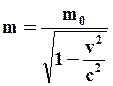(84)

называется массой движущегося тела или релятивистской массой. Из (84) следует, что при 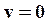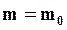; 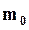называется массой покоя. Она не зависит от скорости тела и является инвариантной величиной.