Интервал.

Всякое событие происходит в пространстве и во времени и характеризуется тремя пространственными координатами x,y,z и одной временной координатой t. Поэтому для изучения динамики различных процессов часто пользуются воображаемым четырехмерным пространством, на осях которого откладывают координаты x,y,z и время t (четырехмерный мир Минковского).

Рассмотрим в четырехмерном пространстве два события: первое имеет координаты x₁, y₁, z₁, t₁, второе – x₂, y₂, z₂, t₂. Величину

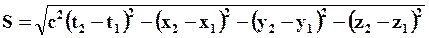(75)

называют интервалом между событиями.

Покажем, что интервал между двумя данными событиями одинаков во всех инерциальных системах отсчета. Для этого запишем (75) в двух инерциальных системах отсчета, движущихся относительно друг друга со скоростью 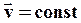, в следующем виде:

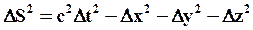(76)

и

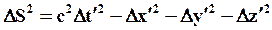(77)

Из преобразований Лоренца следует, что:

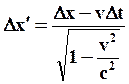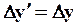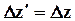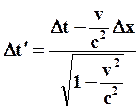; ; ; ; (78)

Подставим (78) а (77)

т.к. 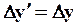; 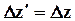, рассмотрим разность :

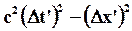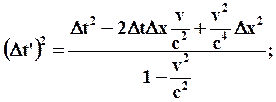
умножим на с²:

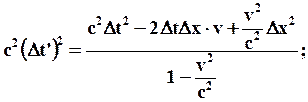
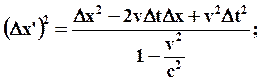
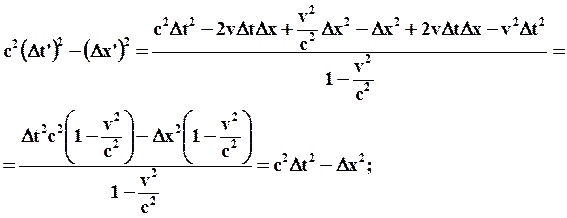
откуда следует, что

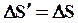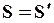или (79)

Понятие интервала устанавливает связь между пространственными и временными координатами событий. Как следует из (79), величина интервала не меняется при переходе от одной инерциальной системы отсчета к другой. Этот вывод вытекает из условия, что скорость света одинакова во всех инерциальных системах. Поэтому (79) представляет собой математическое выражение постулата о постоянстве скорости света.