Уравнение вращательного движения твердого тела относительно точки.
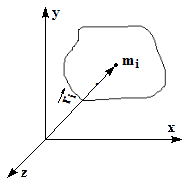
| Будем рассматривать твердое тело, как систему n точек в системе координат xyz.
Обозначим:
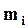 , , 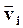 - масса и скорость i-той точки; - масса и скорость i-той точки;
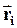 - ее радиус-вектор; - ее радиус-вектор;
 - внутренняя сила, действующая на i-тую точку со стороны k-той; - внутренняя сила, действующая на i-тую точку со стороны k-той;
|
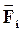 - равнодействующая всех внешних сил, действующих на i-тую точку.
- равнодействующая всех внешних сил, действующих на i-тую точку.
Запишем для i-той материальной точки II закон Ньютона:
 (38)
(38)
Умножим слева обе части (38) векторно на 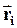 :
:
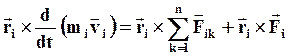 (39)
(39)
Видно, что
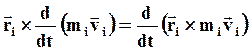 (40)
(40)
В самом деле:
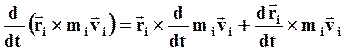
причем:

Перепишем уравнение (39) с учетом (40):
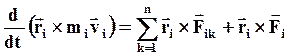 (41)
(41)
Векторное произведение радиус-вектора точки на ее импульс называется моментом импульса точки относительно т. О:
 (42)
(42)
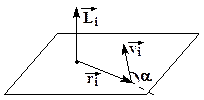
| Направление 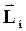 находится по правилу векторного произведения. Для случая на рисунке находится по правилу векторного произведения. Для случая на рисунке 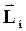 перпендикулярен плоскости, в которой лежат перпендикулярен плоскости, в которой лежат 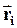 и и 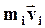 , и направлен вверх. Модуль момента импульса равен: , и направлен вверх. Модуль момента импульса равен:
|
 ,
,  (43)
(43)
Векторное произведение радиус-вектора точки приложения силы на вектор этой силы называется моментом силы относительно т. О.
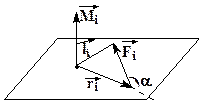
| 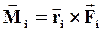 (11)
Направление (11)
Направление 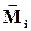 покажем на рисунке.
Модуль момента силы равен: покажем на рисунке.
Модуль момента силы равен: 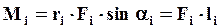 (44)
где (44)
где 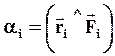 , , 
|
Перпендикуляр 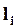 , опущенный из т.О на направление вектора силы, называется плечом этой силы.
, опущенный из т.О на направление вектора силы, называется плечом этой силы.
С учетом (41) и (43) перепишем (40) в виде:
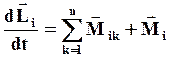 (45)
(45)
Записывая аналогичные уравнения для всех n точек твердого тела и суммируя их почленно, получим:
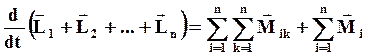 (46)
(46)
Векторная сумма 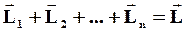 называется моментом импульса тела относительно т. О.
называется моментом импульса тела относительно т. О.
Векторная сумма моментов внешних сил, приложенных ко всем точкам системы, называется результирующим или главным моментом внешних сил относительно т. О:

Наконец, векторная сумма моментов всех внутренних сил относительно т. О равна нулю: 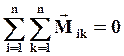 , т.к. момент каждой пары внутренних сил
, т.к. момент каждой пары внутренних сил  и
и 
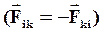 равен нулю. Тогда уравнение (40) примет вид:
равен нулю. Тогда уравнение (40) примет вид:
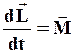 (47)
(47)
Это уравнение называется уравнением вращательного движения твердого тела относительно неподвижной точки.
Дата добавления: 2014-12-09; просмотров: 1066;
