Момент импульса тела относительно неподвижной оси.
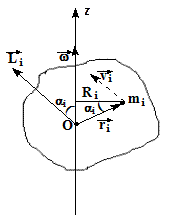
| Рассмотрим i-тую точку твердого тела, вращающегося вокруг неподвижной оси Oz. Если 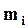 и и 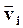 - масса и скорость точки, а - масса и скорость точки, а 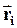 - ее радиус-вектор относительно т. О, то момент импульса - ее радиус-вектор относительно т. О, то момент импульса 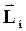 точки равен: точки равен:
 а его модуль:
а его модуль:
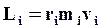
|
Здесь учтено, что векторы 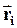 и
и 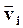 взаимно перпендикулярны
взаимно перпендикулярны 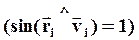 . Проекция момента импульса
. Проекция момента импульса 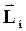 на ось Oz равна:
на ось Oz равна:
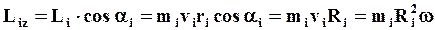
где 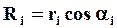 - радиус окружности, по которой движется i-тая точка при вращении тела,
- радиус окружности, по которой движется i-тая точка при вращении тела,
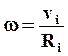 - угловая скорость вращения.
- угловая скорость вращения.
Момент импульса всего тела относительно оси Oz.
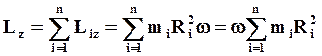 (49)
(49)
Произведение массы точки на квадрат ее кратчайшего расстояния до оси вращения называется моментом инерции точки относительно этой оси:
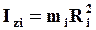 (50)
(50)
Величина:
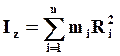 (51)
(51)
называется моментом инерции тела относительно этой оси.
С учетом (51) перепишем (49) в виде:
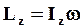 (52)
(52)
Поставим (52) в уравнение (48) вращательного движения тела относительно оси Oz:
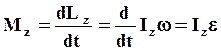
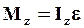 (53)
(53)
Это уравнение справедливо только в том случае, когда  , из сравнения (53) со вторым законом Ньютона
, из сравнения (53) со вторым законом Ньютона 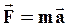 можно сделать вывод, что момент инерции
можно сделать вывод, что момент инерции 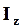 является мерой инерции твердого тела, вращающегося вокруг неподвижной оси.
является мерой инерции твердого тела, вращающегося вокруг неподвижной оси.
Дата добавления: 2014-12-09; просмотров: 1308;
