Моменты инерции однородных тел массой m, имеющих правильную геометрическую форму и равномерное распределение массы по объему

Тело	Положение оси вращения	Момент инерции
Полый тонкостенный цилиндр радиуса R	ось симметрии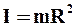
Сплошной цилиндр или диск радиуса R	ось симметрии
Прямой тонкий стержень длиной l	ось перпендикулярна стержню и проходит через его середину
Шар радиусом R	ось проходит через центр шара

Для нахождения момента инерции тела относительно оси, не проходящей через центр тяжести, применяется теорема Штейнера:

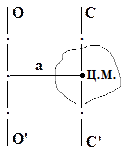
-момент инерции I тела относительно оси OO’ равен моменту инерции I0 тела относительно параллельной ей оси CC’, проходящей через центр масс, сложенному с произведением массы m этого тела на квадрат расстояния aмежду осями: (55)

Например, момент инерции прямого тонкого стержня длиной l относительно оси, которая перпендикулярна стержню и проходит через его конец (эта ось отстоит на l/2 от оси, проходящей через центр стрежня):

Таким образом, величина момента инерции зависит от выбора оси вращения.