Закон сохранения энергии в механике. Общефизический закон сохранения.
Рассмотрим систему материальных точек и обозначим:
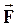 - результирующая всех внешних сил, действующих на систему;
- результирующая всех внешних сил, действующих на систему;
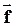 - результирующая всех внутренних консервативных сил;
- результирующая всех внутренних консервативных сил;
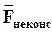 - результирующая всех внутренних неконсервативных сил, действующих на материальные точки.
- результирующая всех внутренних неконсервативных сил, действующих на материальные точки.
Тогда результирующая всех сил:
 (34)
(34)
Умножим (1) скалярно на малое перемещение 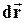 :
:
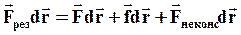 (35)
(35)
Выясним физический смысл:
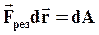 - работа результирующей силы, которая, как было установлено ранее, равна приращению
- работа результирующей силы, которая, как было установлено ранее, равна приращению 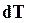 кинетической энергии системы:
кинетической энергии системы:
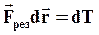
 - работа внешних сил;
- работа внешних сил;
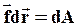 - работа консервативных сил, равная убыли потенциальной энергии системы:
- работа консервативных сил, равная убыли потенциальной энергии системы:
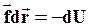
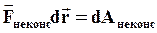 - работа неконсервативных сил.
- работа неконсервативных сил.
Перепишем (35) в виде:
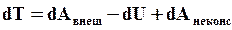
или 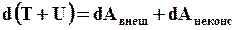 (36)
(36)
Принимая во внимание, что 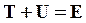 , где
, где  - полная энергия системы, получим:
- полная энергия системы, получим:

Если система замкнута, то на нее внешние силы не действуют и 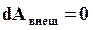 , тогда:
, тогда:

Если в системе не действуют неконсервативные силы, например силы трения, то  и
и
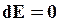 , т.е.
, т.е. 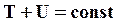 (37)
(37)
(37) – математическая формулировка закона сохранения механической энергии:
- полная энергия замкнутой механической системы не меняется с течением времени.
Однако в реальных системах механическая энергия, отдельно взятая, не сохраняется. В любой реальной системе при движении тел возникают силы трения, которые являются неконсервативными силами. В этом случае  и полная механическая энергия такой системы убывает. Но при этом механическая энергия переходит в различные виды немеханической энергии, например, в энергию теплового движения, т.е. во внутреннюю энергию среды, в которой происходит движение.
и полная механическая энергия такой системы убывает. Но при этом механическая энергия переходит в различные виды немеханической энергии, например, в энергию теплового движения, т.е. во внутреннюю энергию среды, в которой происходит движение.
Поэтому рассмотренный нами закон сохранения и превращения механической энергии является частным случаем всеобщего физического закона сохранения и превращения энергии.
Дата добавления: 2014-12-09; просмотров: 2618;
