Свойства потенциальных полей.
1. Работа в потенциальном поле по замкнутой траектории равна нулю.
2. Потенциальная энергия системы определяется с точностью до некоторой постоянной.
В самом деле, потенциальная энергия, например, тела в поле тяготения Земли 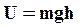 , причем h может быть отсчитано от поверхности Земли, от центра Земли или какой-нибудь точки. В зависимости от этого меняется значение U. Поэтому, определяя потенциальную энергию, необходимо условиться, при каком взаимном расположении тел их взаимная потенциальная энергия равна нулю.
, причем h может быть отсчитано от поверхности Земли, от центра Земли или какой-нибудь точки. В зависимости от этого меняется значение U. Поэтому, определяя потенциальную энергию, необходимо условиться, при каком взаимном расположении тел их взаимная потенциальная энергия равна нулю.
3. Связь потенциальной энергии с силой, действующей на данную точку.
Рассмотрим произвольное потенциальное поле U(x,y,z), в котором действуют силы 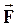 .
.
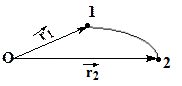
| Работа по перемещению частицы из т.1 в т.2 силами этого поля равна:
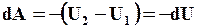 С другой стороны, та же работа запишется в виде:
С другой стороны, та же работа запишется в виде:
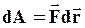
|
получим:
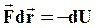 (30)
(30)
Запишем это равенство в координатах. Как известно:
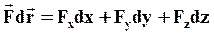
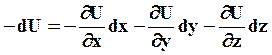
тогда: 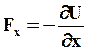 ;
; 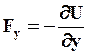 ;
; 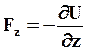 (31)
(31)
Вектор с компонентами 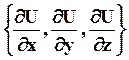 называется градиентом функции U и обозначается
называется градиентом функции U и обозначается 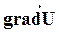 . В векторной форме (30) запишется в виде:
. В векторной форме (30) запишется в виде:
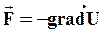
Итак, сила, действующая на материальную точку в потенциальном поле, равна взятому с обратным знаком градиенту потенциальной энергии этой точки в рассматриваемом поле.
Пример 1. Потенциальная энергия упругодеформированного тела.

| При достаточно медленном растяжении пружины внешней силой Fвн на величину x в ней возникает упругая сила Fупр, которая по закону Гука равна:
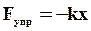 где k – коэффициент упругости
где k – коэффициент упругости
|
Работа, совершаемая силой упругости при возвращении пружины в недеформированное состояние, найдется интегрированием:
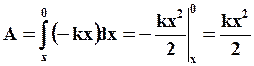
Силы упругости являются потенциальными силами, поэтому:
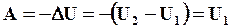
(в недеформированном состоянии потенциальная энергия пружины U2=0). Отсюда:
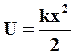 (32)
(32)
Пример 2. Потенциальная энергия тяготения.
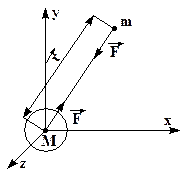
| Рассмотрим 2 тела массами M и m, которые взаимодействуют по закону всемирного тяготения:
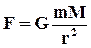 Предположим, что тело M неподвижно. Работа, совершаемая силой тяготения при приближении
тела m к телу M от расстояния r1 до расстояния r2, равна:
Предположим, что тело M неподвижно. Работа, совершаемая силой тяготения при приближении
тела m к телу M от расстояния r1 до расстояния r2, равна:
|
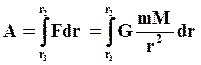
При сближении тел dr<0. Учитывая знак dr, получим:
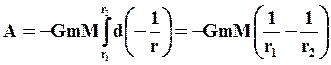
Учитывая, что 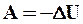 , найдем, что потенциальная энергия гравитационного взаимодействия двух тел Mи m, находящихся на расстоянии r друг от друга, равна:
, найдем, что потенциальная энергия гравитационного взаимодействия двух тел Mи m, находящихся на расстоянии r друг от друга, равна:
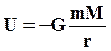 (33)
(33)
Отрицательное значение потенциальной энергии связано с тем, что за начало отсчета Uпринято ее значение в бесконечности, где силы взаимодействия между телами m и М практически отсутствуют, т.е. 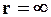 ,
, 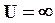 . При перемещении тела m из бесконечности в данную точку поля силами тяготения совершается работа за счет убыли потенциальной энергии этих тел. Следовательно, при любом
. При перемещении тела m из бесконечности в данную точку поля силами тяготения совершается работа за счет убыли потенциальной энергии этих тел. Следовательно, при любом 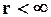 Uдолжна быть меньше U¥, т.е. потенциальная энергия должна быть отрицательной.
Uдолжна быть меньше U¥, т.е. потенциальная энергия должна быть отрицательной.
Потенциальная энергия тела, находящегося на поверхности Земли (r=R), равна:
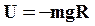
Учтем, что 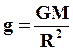
Потенциальную энергию тела, поднятого на небольшую высоту h (h<<R), можно представить следующим образом:
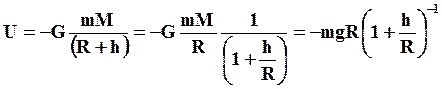
(т.к. 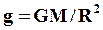 )
)
Разложим выражение в скобке в ряд и отбросим члены второго порядка малости:
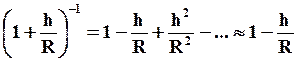
Тогда:
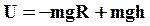
Полагая потенциальную энергию тела на поверхности Земли равной нулю, получим хорошо известное выражение:
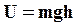
Дата добавления: 2014-12-09; просмотров: 3264;
