Тангенциальное и нормальное ускорение.
При криволинейном движении происходит изменение скорости, как по величине, так и по направлению. Принимая во внимание, что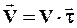 
, представим 
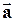в виде суммы двух векторов:
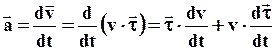(6)
Первое слагаемое характеризует изменение скорости по величине и называется тангенциальным ускорением:
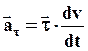(7)
Численное значение тангенциального ускорения равно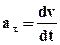 
, а направление совпадает с направлением касательной к траектории движения.
Второе слагаемое характеризует изменение скорости по направлению и называется нормальным ускорением:
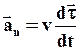(8)
Численное значение нормального ускорения равно:
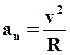(9)
R– радиус кривизны траектории в точке, где определяется ускорение. Направление совпадает с нормалью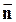 
к траектории.
Разложение ускорения на тангенциальное и нормальное поясним рисунком. Представим вектор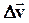 
в виде суммы двух векторов, для чего вдоль направления 
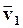отложим длину AL вектора 
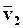и соединим точки D и L. Из рисунка видно, что 
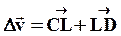, причем вектор 
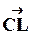дает изменение скорости по величине 
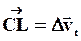, а вектор 
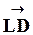- по направлению 
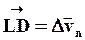. Тогда 
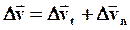. Разделим почленно на Dt и перейдем к пределу Dt®0:
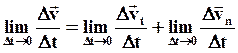
тогда получим, что полное ускорение точки равно:
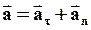(10)
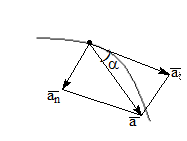
| По модулю полное ускорение равно:
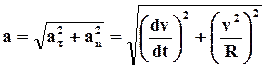Направление определяется углом a:
|
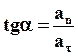
Самый простой вид неравномерного движения – равноускоренное движение. Равноускоренным называется движение с постоянным по модулю и направлению ускорением.
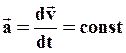
При равноускоренном движении с начальной скоростью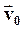 
ускорение равно:
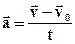
где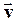 
- скорость в момент времени t.
Отсюда скорость равноускоренного движения:
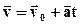
Дата добавления: 2014-12-09; просмотров: 1033;