Равномерное движение по окружности
Рассмотрим наиболее простой вид вращательного движения, и уделим особое внимание центростремительному ускорению.
При равномерном движении по окружности значение скорости остается постоянным, а направление вектора скорости 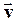 изменяется в процессе движения.
изменяется в процессе движения.
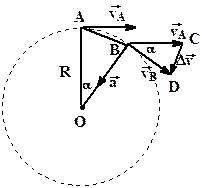
| За интервал времени ∆t тело проходит путь 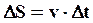 . Этот путь равен длине дуги AB. Векторы скоростей . Этот путь равен длине дуги AB. Векторы скоростей 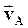 и и 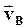 в точках A и Bнаправлены по касательным к окружности в этих точках, а угол a между векторами в точках A и Bнаправлены по касательным к окружности в этих точках, а угол a между векторами 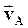 и и 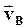 равен углу между радиусами OA и OB. Найдем разность векторов равен углу между радиусами OA и OB. Найдем разность векторов 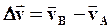 и определим отношение изменения скорости к ∆t: и определим отношение изменения скорости к ∆t:
|
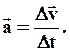
Из подобия треугольников OAB и BCD следует
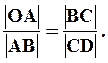
Если интервал времени ∆t мал, то мал и угол a. При малых значениях угла a длина хорды AB примерно равна длине дуги AB, т.е. 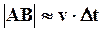 . Т.к.
. Т.к. 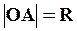 ,
, 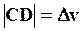 , то получаем
, то получаем
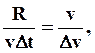
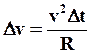 .
.
Поскольку 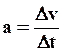 , то получаем
, то получаем
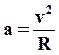
Дата добавления: 2014-12-09; просмотров: 1089;
