Скорость материальной точки.
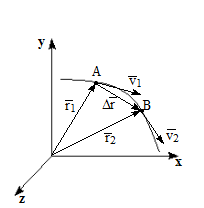
| Пусть при движении по криволинейной траектории материальная точка в некоторый момент времени t1занимала положение Aс радиус-вектором 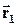 , а в момент времени t2=t1+Dt – положение B с радиус-вектором , а в момент времени t2=t1+Dt – положение B с радиус-вектором 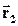 . За время Dt=t2-t1 радиус-вектор получил приращение . За время Dt=t2-t1 радиус-вектор получил приращение 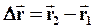 . .
|
Средней векторной скоростью материальной точки называют отношение приращения радиус-вектора точки к тому промежутку времени, за которые это приращение произошло:
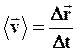 (1)
(1)
Средняя путевая скорость:
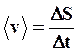
В Международной системе (СИ) единицей расстояния является метр, единицей времени – секунда, поэтому скорость выражается в метрах в секунду:
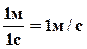
Если 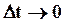 , то отношение
, то отношение 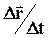 стремится к некоторому пределу, называемому скоростью материальной точки в момент времени t или мгновенной скоростью
стремится к некоторому пределу, называемому скоростью материальной точки в момент времени t или мгновенной скоростью 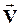 :
:
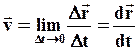 (2)
(2)
Мгновенной скоростью точки называют вектор, численно равный первой производной по времени от радиус-вектора, определяющего положение этой точки в данный момент времени. Вектор 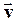 направлен по касательной к траектории в этой точке, т.е.:
направлен по касательной к траектории в этой точке, т.е.:
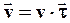 (3)
(3)
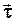 - единичный вектор касательной к траектории в данной точке;
- единичный вектор касательной к траектории в данной точке;
v– модуль скорости, равный:
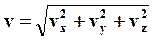 .
.
Движение с постоянной по модулю и направлению скоростью называется прямолинейным равномерным движением.
При прямолинейном движении (по модулю):
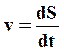
В реальных условиях движение любого тела никогда не бывает строго равномерным и прямолинейным. Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным движением.
Дата добавления: 2014-12-09; просмотров: 843;
