ВЛИЯНИЕ РАСТВОРИТЕЛЕЙ НА СКОРОСТЬ ХИМИЧЕСКИХ РЕАКЦИЙ
Кинетика: влияние растворителя на скорость реакции Меншуткина:
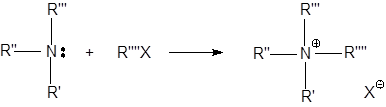
(C3H7)3N + CH3I  [(C3H7)3N [(C3H7)3N 
|
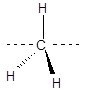
|
I 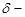 ] ] 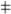  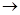 (C3H7)4N+ + I– (C3H7)4N+ + I–
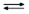 (C3H7)4N+I– (C3H7)4N+I–
|
Дипольные моменты три-н-пропиламина и иодметана составляют соответственно 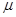 = 0.70 Дб и 1.64 Дб, в то время как у активированного комплекса
= 0.70 Дб и 1.64 Дб, в то время как у активированного комплекса 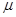 = 8.7 Дб. В итоге скорость этой реакции кватернизации при 20 оС возрастает по сравнению с реакцией в н-гексане в 120 раз в диэтиловом эфире, в 13 000 раз в трихлорметане и в 110 000 в нитрометане.
= 8.7 Дб. В итоге скорость этой реакции кватернизации при 20 оС возрастает по сравнению с реакцией в н-гексане в 120 раз в диэтиловом эфире, в 13 000 раз в трихлорметане и в 110 000 в нитрометане.
Скорость химической реакции, протекающей в растворе, существенно зави-
сит от свойств растворителя. Изучение закономерностей влияния растворителей
на реакции алифатического нуклеофильного замещения позволили Хьюзу и Ин-
гольду сформулировать эмпирические правила, которые на качественном уровне
описывают зависимость скорости реакции от свойств среды:
а) повышение полярности растворителя приводит к росту скорости реак-
ций, в которых активированный комплекс имеет бoльшую плотность заряда, чем
исходная молекула (или молекулы);
б) повышение полярности растворителя приводит к снижению скорости ре-
акций, в которых плотность заряда в активированном комплексе меньше, чем в
исходной молекуле (или молекулах);
в) изменение полярности растворителя практически не влияет на скорость
реакций, в которых плотность заряда исходных веществ и активированного ком-
плекса остается постоянной или изменяется незначительно.
Другими словами, замена менее полярного растворителя на более полярный
приведет к повышению или снижению скорости реакции в зависимости от того,
имеет ли активированный комплекс большую или меньшую плотность заряда по
сравнению с исходными веществами. Под "полярностью" растворителя здесь
понимают его способность сольватировать находящиеся в растворе заряженные
частицы. Считается, что сольватирующая способность растворителя повышается
при увеличении дипольного момента его молекул.
Объяснение правил Хьюза.Ингольда может быть дано при помощи про-
стой модели сольватации, учитывающей только электростатические взаимодей-
ствия между реагирующими ионами (или биполярными молекулами) и молеку-
лами растворителя как в начальном, так и в переходном состояниях. Несмотря на
чрезвычайно широкое и успешное применение этих правил, им свойственны оп-
ределенные ограничения и недостатки. Можно считать, что все исключения из
правил Хьюза.Ингольда обусловлены сильными специфическими взаимодейст-
виями растворителя с веществами, находящимися в растворе, например за счет
образования водородных или донорно-акцепторных связей.
Простейшее количественное описание влияния растворителя на скорость
реакции может быть дано на основе теории переходного состояния, согласно
которой реакция между ионами А и В протекает через равновесное образование
активированного комплекса XЃ‚ , который затем распадается на продукты реак-
ции
A B X Продукты Ѓ‚ + ЃЁ . (1)
Скорость образования продуктов реакции пропорциональна равновесной
концентрации активированного комплекса
v
1[X ] v k Ѓ‚ = , (2)
Физическая химия неводных растворов
где – константа скорости распада активированного комплекса на продукты
реакции.
1 k
Константа равновесия образования активированного комплекса определяется
активностями соответствующих частиц
[X ]
[A][B]
X X
AB A
a
K
a a B
Ѓ‚ Ѓ‚ Ѓ‚ .
= = .
. .
. (3)
Если выразить концентрацию активированного комплекса из уравнения (3),
[X ] [A][B] A B
X
K
Ѓ‚
Ѓ‚ . .
= .
.
, (4)
и подставить полученное выражение в уравнение (2), то для скорости реакции
получим
1 [A][B] [A][B] A B
X
v kK k
Ѓ‚
. .
= . =
.
. (5)
Таким образом, экспериментально определяемая константа скорости реакции
зависит от коэффициентов активности реагентов и активированного комплекса
1 0
AB A
X X
k kK k B
Ѓ‚ Ѓ‚
. . . .
= =
. .
, (6)
где – константа скорости в реальном растворе, a – константа скорости в
стандартном растворителе при данной температуре, когда коэффициенты актив-
ности участников реакции равны единице. Логарифмируя выражение
k 0 k
(6) имеем
0 ln ln ln ln ln A B X k k Ѓ‚ = + . + . . . . (7)
Если в качестве стандартного состояния выбрать состояние иона в вакууме, в
котором диэлектрическая проницаемость равна единице, то при пренебрежении
неэлектростатическими вкладами в энергию сольватации коэффициент активно-
сти иона в растворе с бесконечно малой ионной силой будет определяется выра-
жением
2 2 1 ln 1
i
i
z e
akT
. . = . .. . .
.
., (8)
где – заряд частицы, – заряд электрона, i z e . – диэлектрическая проницае-
мость растворителя, – радиус частицы, . константа Больцмана, – абсо-
лютная температура.
a k T
Подставляя выражение (8) в уравнение (7), имеем
2 2 2
1 ( ln ln 1
A B A B
A B X
e z z z z k k
kT r r r Ѓ‚
. . + . . = + . + . . . . .. . . . .. .
2), (9)
где A z и – заряды реагирующих частиц, B z , , A B X r r r Ѓ‚ . радиусы реагирующих
частиц и активированного комплекса.
Влияние растворителя на константу скорости химической реакции
Уравнение (9), называемое уравнением Лейдлера.Эйринга, предсказывает ли-
нейную зависимость константы скорости реакции от величины обратной диэлек-
трической проницаемости растворителя. Если предположить, что радиусы реа-
гирующих частиц и активированного комплекса примерно одинаковы, то есть
принять, что
A B X r r r Ѓ‚ R ЎЦ ЎЦ = , (10)
то уравнение (9) можно преобразовать к виду, известному как уравнение Скэт-
чарда
1 ln ln 1 A B z z e k k
kTR
. . = . .. . .
... (11)
Величину R в уравнении (11) называют радиусом реакции или радиусом акти-
вированного комплекса. Уравнение (11), дает возможность предсказывать знак
производной
2 ln
(1/ )
A B k zz
kTR
ЃЭ
= .
ЃЭ .
e , (12)
а на основании величины производной . рассчитывать значение R. Очевидно,
что если в реакцию вступают ионы с одинаковым знаком заряда, то логарифм
константы ее скорости будет линейно снижаться с ростом величины 1/ раство-
рителя, если же заряды реагирующих ионов имеют разные знаки, то в этом слу-
чае должно наблюдаться линейное увеличение с ростом 1/ . Другими сло-
вами, снижение диэлектрической проницаемости растворителя ускоряет реак-
ции, протекающие между противоположно заряженными ионами, и замедляет
реакции с участием одинаково заряженных частиц. Учитывая, что диэлектриче-
ская проницаемость может использоваться в качестве характеристики полярно-
сти растворителя, уравнения
.
ln k .
(9), (11) и (12), фактически, являются математиче-
ским выражением правил Хьюза.Ингольда.
Экспериментальные данные, полученные для реакций, в которых замена
растворителя не изменяет механизма реакции, находятся в хорошем соответст-
вии с уравнениями (9), (11) и (12). В качестве примера, подтверждающего спра-
ведливость этих уравнений, можно привести рисунок 1, взятый из статьи, в ко-
торой было изучено влияние диэлектрической проницаемости смешанного рас-
творителя вода-диоксан на константу скорости взаимодействия ряда красителей
с гидроксид-ионом. Из графика, приведенного на рис.1, хорошо видна линей-
ность зависимости от 1 lg k / . , что позволило авторам статьи вычислить радиус
активированного комплекса, используя уравнение (12).
Ограничения в применимости уравнений (9), (11) и (12) таковы же как и
для правил Хьюза.Ингольда . наличие сильных специфических взаимодейст-
виями растворителя и реагирующих веществ. Также следует отметить, что если
Синев В.В. и др. О приложимости электростатической теории к кинетике реакции типа анион- анион
в триарилметановом ряду. Деп. ВИНИТИ, Л., 1985. 13 с.
Физическая химия неводных растворов
для исследования используются смешанные растворители, то зависимость
от 1 может отклоняться от линейности вследствие избирательной сольватации
реагентов или активированного комлекса одним из компонентов растворителя.
ln k
/ .
Рис. 1. Зависимость от величины lg k 1/ . для реакции некоторых
красителей с гидроксид ионом в системе смешанных растворителей
вода-диоксан: I . бромфеноловый синий, II . фенолфталеин, III .
о-крезолфталеин, IV . 3,3'-диметоксибензаурин
При выводе уравнения (9) предполагалось, что ионная сила раствора, в ко-
тором протекает реакция, бесконечно мала. Если же это не так, то наличие соле-
вого эффекта, описываемого уравнением Бренстеда–Бьеррума
0 ln ln 2 A B k k Azz = + I, (13)
где . ионная сила раствора, может влиять на величину константы скорости.
Поэтому для построения зависимостей от 1
I
ln k / . используются данные по кон-
стантам скорости, экстраполированные на нулевую ионную силу, или соответст-
вующие одному и тому же значению раствора. I
Литература
1. Глесстон Г., Лейдлер К., Эйринг Г. Теория абсолютных скоростей реакций. М.:
Изд-во иностранной литературы, 1948. 583 с.
2. Амис Э. Влияние растворителя на скорость и механизм химических реакций.
М.: Мир, 1968. 328 с.
3. Мелвин-Хьюз Е.А. Равновесие и кинетика реакций в растворах. М.: Химия,
1975. 472 с.
4. Эйринг Г., Лин С.Г., Лин С.М. Основы химической кинетики. М.: Мир, 1983.
528 с.
5. Райхардт К. Растворители и эффекты среды в органической химии. М.: Мир,
1991. 783 с.
Полярность растворителя является не единственным фактором, влияющим на скорость реакции. Существенную роль играют специфические взаимодействия с растворителем (или их отсутствие). Например, реакция
F– + CH3I 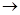 CH3F + I–
CH3F + I–
идет в диметилсульфоксиде в десять миллионов раз быстрее, чем в спирте. Очевидной причиной здесь является плохая сольватация фторид-иона в полярном НДВС-растворителе и хорошая – в спиртах, являющихся донорами водородной связи.
С другой стороны, разрыв связи углерод–галоген в соединениях типа триарилгалогенметана облегчается в воде и спиртах за счет сольватации переходного состояния и продукта реакции – иона галогена:
R–X + HO–R/ 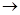 [R
[R 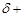 ···X
···X 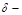 ··· HO–R/ ]
··· HO–R/ ] 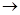 R+ + X–··· HO–R/
R+ + X–··· HO–R/
Дата добавления: 2014-12-09; просмотров: 6566;
