Коэффициент корреляции.

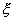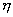Как мы знаем, если и - независимые случайные величины, то по свойству математического ожидания (§ 4, п. 1)

(72)

Если же 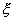и 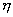не являются независимыми случайными величинами, то, вообще говоря,

Условились за меру связи (зависимости) двух случайных величин 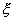и 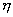принять безразмерную величину , определяемую соотношением.

(73)

и называемую коэффициентом корреляции.

Рассмотрим некоторые свойства коэффициента корреляции.
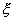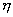Если и - независимые случайные величины, то коэффициент корреляции равен нулю.
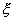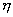Это свойство непосредственно вытекает из соотношений (72) и (73). Заметим, что обратное утверждение, вообще говоря, неверно, т. е. если , то отсюда еще не следует, что и независимы.
Заметим без доказательства, что 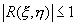. При этом если 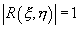, то между случайными величинам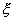и и 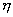имеет место функциональная, а именно линейная зависимость.

Замечание. Как мы видели (§ 3, п. 6), двумерная случайная величина распределена нормально, если плотность 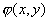распределения системы величин и имеет вид

Можно показать, что постоянная R равна коэффициенту корреляции величин и , т.е. 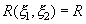. Следует заметить, что в случае, когда система величин и распределена нормально и коэффициент корреляции , то величины и независимы (см. § 3, п. 6)