Функции и линии регрессии.
Пусть 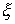 и
и  - две случайные непрерывные величины, находящиеся в корреляционной зависимости. Это значит, что каждому значениюx случайной величины
- две случайные непрерывные величины, находящиеся в корреляционной зависимости. Это значит, что каждому значениюx случайной величины 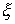 соответствует вполне определенное распределение вероятностей величины
соответствует вполне определенное распределение вероятностей величины  . Плотность
. Плотность 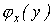 распределения величины
распределения величины  при условии, что
при условии, что 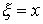 , называется условной плотностью распределения случайной величины
, называется условной плотностью распределения случайной величины  .
.
Вычислим для данного случая так называемое условное математическое ожидание 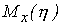 величины
величины  при условии, что
при условии, что 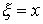 .Согласно определению математического ожидания непрерывной случайной величины, имеем
.Согласно определению математического ожидания непрерывной случайной величины, имеем

[см. формулу (40)]. Каждому возможному значению x случайной величины 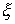 соответствует определенное значение условного математического ожидания
соответствует определенное значение условного математического ожидания 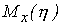 . Таким образом, мы получаем функцию
. Таким образом, мы получаем функцию  переменной x. Эта функция y=f(x)называется функцией регрессии величины
переменной x. Эта функция y=f(x)называется функцией регрессии величины  на
на 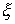 , а ее график - линией регрессии
, а ее график - линией регрессии  на
на 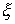 .
.
Аналогично определяется условное математическое ожидание величины 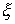 при условии, что
при условии, что 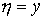 :
:
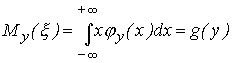
где 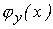 - условная плотность вероятности случайной величины
- условная плотность вероятности случайной величины 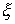 при условии, что
при условии, что 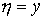 .
.
Функция x=g(y) называется функцией регрессии величины 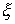 на
на  , а ее график - линией регрессии
, а ее график - линией регрессии 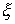 на
на  .
.
Cледует иметь в виду, что функции y=f(x) и x=g(y) не являются обратными по отношению друг к другу.
Если обе функции  и
и  линейны, то линиями регрессии являются прямые. В этом случае говорят, что случайные величины
линейны, то линиями регрессии являются прямые. В этом случае говорят, что случайные величины 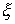 и
и  связаны линейной корреляционной зависимостью. Можно показать, что уравнение прямой регрессии
связаны линейной корреляционной зависимостью. Можно показать, что уравнение прямой регрессии  на
на 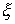 имеет следующий вид:
имеет следующий вид:
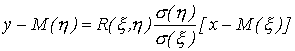
| (74) |
где 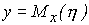 - условное математическое ожидание случайной величины
- условное математическое ожидание случайной величины  при
при 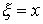 . Аналогично записывается уравнение прямой регрессии
. Аналогично записывается уравнение прямой регрессии 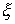 на
на  :
:
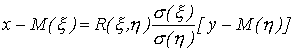
| (75) |
где 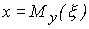 - условное математическое ожидание случайной величины
- условное математическое ожидание случайной величины 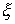 при
при 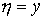 .
.
Величины
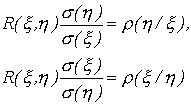
| (76) |
называются коэффициентами регрессии соответственно  на
на 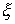 и
и 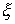 на
на  .
.
Из формул (76) следует, что
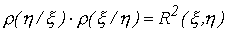
| (77) |
Равенство (77) показывает, что оба коэффициента регрессии имеют одинаковые знаки. Если они положительны (отрицательны), то с возрастанием аргумента возрастают (убывают) соответствующие условные математические ожидания.
Если 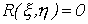 , то, как следует из уравнений (74) и (75),
, то, как следует из уравнений (74) и (75), 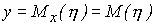 и
и  , т.е. в этом случае условные математические ожидания постоянны и равны соответствующим математическим ожиданиям случайных величин
, т.е. в этом случае условные математические ожидания постоянны и равны соответствующим математическим ожиданиям случайных величин  и
и 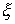 .
.
Замечание. Можно доказать, что если система двух случайных величин имеет нормальное распределение, то эти величины находятся в линейной корреляционной зависимости.
Дата добавления: 2014-11-29; просмотров: 1234;
