Расстояние от точки до прямой

Теорема. Если задана точка М(х₀, у₀), то расстояние до прямой Ах + Ву + С =0 определяется как

.

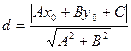Пример. Определить угол между прямыми: y = -3x + 7; y = 2x + 1.

Решение. k₁ = -3; k₂ = 2 tgj = 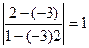; j = p/4.

Пример.Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.

Решение.Находим: k₁ = 3/5, k₂ = -5/3, k₁k₂ = -1, следовательно, прямые перпендикулярны.

Решение типового примера. Пусть А(-1; 2), В(5; -1), С(-4; -5).

1. Расстояние d между точками А{х₁;у₁) и В(х₂; у₂)определяется по формуле

d = 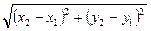, (1)

воспользовавшись которой находим длину стороны АВ:

АВ = .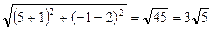

2. Уравнение прямой, проходящей через две заданные точки плоскости А(х₁;у₁) и В(х₂; у₂) имеет вид

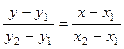(2)

Подставляя в (2) координаты точек А и В,получаем уравнение стороны АВ:

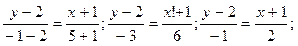
2у - 4= - х – 1; х+22у-3=0 (АВ)

 

Угловой коэффициент k_АВ прямой АВ найдем, преобразовав полученное уравнение к виду уравнения прямой с угловым коэффициентом

y = kx + b.

У нас 2у = - х+3, то есть у= 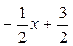откуда k_АВ = .

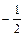Аналогично получим уравнение прямой ВС и найдем ее угловой коэффициент:

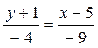; - 9у - 9=-4х+20

—4х—9у—29=0 (ВС).

Далее -9у=-4х+29; у= 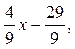т.е. k_ВС= .

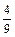3. Для нахождения внутреннего угла нашего треугольника воспользуемся формулой

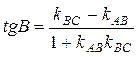(3)

 

Отметим, что порядок вычисления разности угловых коэффициентов, стоящей в числителе этой дроби, зависит от взаимного расположения прямых АВ и ВС. Подставив ранее вычисленные значения k_АВ и k_ВС в (3), находим:

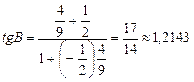
Теперь, воспользовавшись таблицами В. М. Брадиса или инженерным микрокалькулятором, получаем В 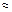0,88 рад.

4. Для составления уравнения медианы АЕнайдем сначала координаты точки Е, которая лежит на середине отрезка ВС:

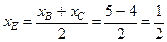
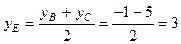
Теперь, подставив в (2) координаты точек А и Е,получаем уравнение медианы:

;

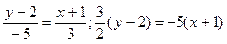3(у-2)=-10(х+1); 10х+3у+4=0 (АЕ).

5. Для составления уравнения высоты CD воспользуемся уравнением прямой, проходящей через заданную точку М₀{х₀,у₀)с заданным угловым коэффициентом k,которое имеет вид

у—y₀=k(x—хо),(4)

и условием перпендикулярности прямых АВ и CD, которое выражается соотношением k_AB *k _CD= - 1, откуда k _CD= 2. Подставив в (4) вместо kзначение k _CD= 2, а вместо х₀, у_окоординаты точки С, получим уравнение высоты CD:

у+5 = 2(х+4); у+5 = 2х+8; 2х-у + 3=0 (CD).

Для вычисления длины высоты CD воспользуемся форму­лой отыскания расстояния d от заданной точки Мо{х₀, у₀)до заданной прямой с уравнением Ах+Ву-С=0, которая имеет вид

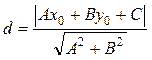(5)

Подставив в (5) вместо х_о, у_о координаты точки С, а вместо А, В и Скоэффициенты уравнения прямой АВ, получаем

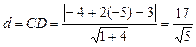
6. Так как искомая прямая EFпараллельна прямой АВ, то k_EF =k_AB = 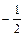. Подставив в уравнение (4) вместо х₀,у₀ координаты точки Е, а вместо k значение k_EF получаем уравнение прямой ЕЕ:

у+3= 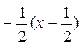;2у+6= -х + ;

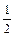4у+12= -2х+1; 2х+4у+11=0 (EF).

Для отыскания координат точки М решаем совместно уравнения прямых EF и CD:

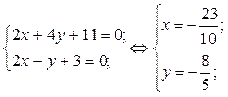
Таким образом, М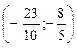

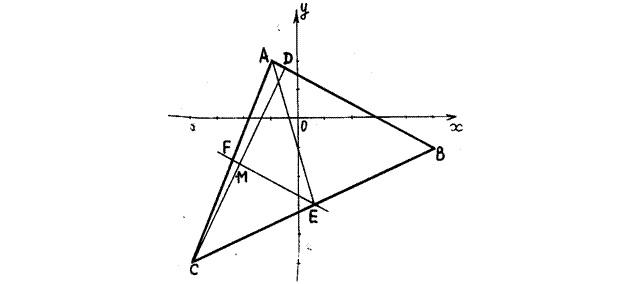
Треугольник ABC, высота CD, медиана АЕ, прямая EF и точка М построены в системе координат хОу на рисунке.

 

Вопросы для самопроверки

1. Как определяются декартовы координаты точки на плоскости?
2. Чем отличаются координаты двух точек, симметричных относительно: а) оси Ох; б) оси Оу; в) начала координат?
3. Как вычислить расстояние между двумя точками?
4. Напишите формулы для координат середины отрезка через координаты его концов.
5. Напишите формулы для координат точки пересечения медиан треугольника через координаты его вершин.
6. Дайте определение уравнения линии на плоскости.
7. Как найти координаты точки пересечения двух линий на плоскости, заданных своими уравнениями?
8. Чем отличается уравнение прямой в декартовых координатах от уравнений других линий?
9. Напишите формулу для вычисления угла между двумя прямыми.
10. Как выглядит условие параллельности и перпендикулярности двух прямых?
11. Напишите уравнение прямой, проходящей: а) через заданную точку в заданном направлении; б) через две заданные точки.
12. Как написать уравнение медианы, высоты в треугольнике, если известны координаты его вершин?
13. Сформулируйте определения эллипса, гиперболы, параболы. Каковы канонические уравнения этих линий?
14. Что называется эксцентриситетом эллипса и гиперболы, и какие значения он может иметь для каждой из этих линий?