Свойства определителей

1. det (A ± B) = det A ± det B.

2. det (AB) = detA×detB

3.Если в квадратной матрице поменять местами какие-либо две строки (или столбца), то определитель матрицы изменит знак, не изменившись по абсолютной величине.

4.При умножении столбца (или строки) матрицы на число ее определитель умножается на это число.

Определение.Столбцы (строки) матрицы называются линейно зависимыми, если существует их линейная комбинация, равная нулю, имеющая нетривиальные (не равные нулю) решения.

5.Если в матрице А строки или столбцы линейно зависимы, то ее определитель равен нулю.

6.Если матрица содержит нулевой столбец или нулевую строку, то ее определитель равен нулю. (Данное утверждение очевидно, т.к. считать определитель можно именно по нулевой строке или столбцу.)

7.Определитель матрицы не изменится, если к элементам одной из его строк (столбца) прибавить(вычесть) элементы другой строки(столбца), умноженные на какое-либо число, не равное нулю.

Пример. Вычислить определитель матрицы

А =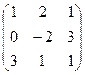

Решение.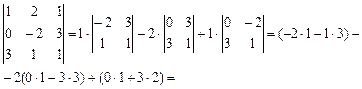

= -5 + 18 + 6 = 19.