Уравнение прямой по точке и направляющему вектору

Определение. Каждый ненулевой вектор 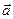(a₁, a₂), координаты которого удовлетворяют условию Аa₁ + Вa₂ = 0 называется направляющим вектором прямой

Ах + Ву + С = 0.

Пример. Найти уравнение прямой с направляющим вектором 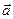(1, -1) и проходящей через точку А(1, 2).

Решение.Уравнение искомой прямой будем искать в виде Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:

1×A + (-1)×B = 0, т.е. А = В.

Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C/A = 0. При х = 1, у = 2 получаем С/A = -3, то есть искомое уравнение х + у - 3 = 0