Приклад 4. Контрольний лист для визначення причин чи місць
походження дефектів.
Для простих випадків можна фіксувати необхідні дані відразу в контрольному листку. На рис. 11 представлена контрольна карта для реєстрації дефектів у виробі, із зазначенням верстатів, працівників, днів виготовлення та типів дефектів. Аналіз карти показує, що працівник В припускається багатьох помилок (дефектів). Всі працівники допускають багато дефектів саме в середу. Дослідження причин дефектів показало, що працівник В недостатньо часто змінює штампи, а причиною дефектів, що допускаються в середу послужила погана якість сировини виробу в цей день.
Крім наведених прикладів, існує велика кількість інших контрольних листів та форм, що використовуються у виробництві. Вони розробляються перш за все з урахуванням мети збору даних, а далі створюються модифікації, що підходять для поставлених цілей та полегшення збору та реєстрації даних.
Дійсні причини браку відшукуються шляхом співставлення дефектів, які є симптомами неякості, з можливими причинами їх появи. При аналізі можуть використовуватись діаграми розсіювання (кореляції) та групування даних за різними ознаками (стратифікація).
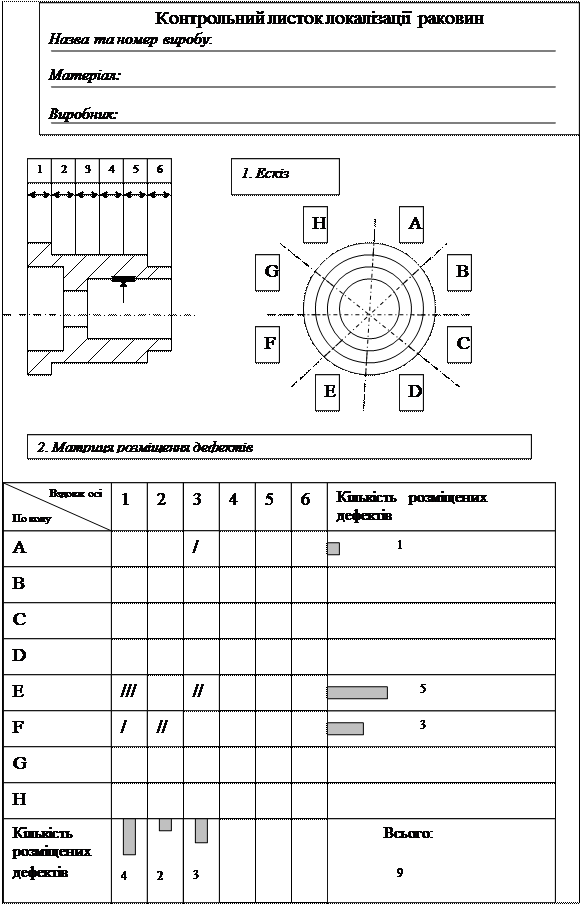
Рис.10. Контрольний листок локалізації дефектів( раковин)
.
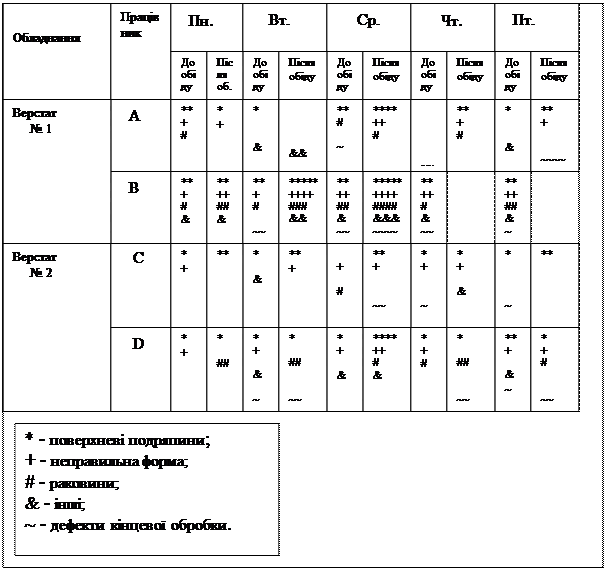
Рис. 11. Контрольний листок реєстрації характеру, причин або місць виникнення дефектів.
Завдання для самостійної роботи.
Використовуючи форму на рис. 11, розробити контрольний листок для реєстрації причини виникнення відмов певної деталі, вузла, агрегату або автомобіля в цілому.
6.2. Гістограми
Гістограма є графічним зображенням результатів вимірювання деякого параметра. Вона представляє собою стовпцевий графік, побудований на основі отриманих за певний період даних. Звичайно, гістограми будують за таблицями даних.
Графічно гістограма являє собою сукупність прямокутників, які мають загальну базу та розташовані сторона до сторони. Бази прямокутників однакові. Вони представляють собою цілі числа або інтервали вимірювання. Висота кожного прямокутника пропорційна кількості випадків вимірювання в даному інтервалі.
Метою побудови гістограми є графічне зображення табличної інформації, яке дозволяє миттєво оцінити характер розподілу експериментальних даних.
Цілочислові бази можуть представляти собою дні, місяці, роки і т.п. По вертикалі відкладають кількість однорідних подій, які мали місце в цей день або місяць, наприклад, кількість скарг по днях тижня, кількість запитів клієнтів по днях, починаючи з моменту виходу реклами і т.д.
Якщо вимірюваний параметр є безперервною величиною, спочатку визначають розмах розподілу як різницю між максимальним та мінімальним значеннями параметра, а потім розбивають цю величину на ряд інтервалів - класів або розрядів.
Є різні рекомендації щодо вибору кількості інтервалів. Наприклад, їх кількість може становити 10% загальної кількості даних. Кількість інтервалів може наближатися до квадратного кореня від загальної кількості даних, якщо така не перевищує 100.
Дані для побудови гістограми розподілу напрацювання на відмову деякої деталі автомобіля наведені в табл. 2. Гістограма розподілу напрацювання на відмову цієї деталі показана на рис.12. На цій гістограмі частота попадання в розряд визначається як відношення кількості випадків попадання в розряд до загальної кількості випадків.
Таблиця 2.
Дані для побудови гістограми розподілу напрацювання на відмову
деталі автомобіля
| Номер інтервалу | Інтервал розрядів, тис.км | Середнє значення інтервалу, тис.км | Реєстрація попадань у інтервал | Кількість попадань у інтервал | Частота попадання у інтервал, f |
| 4 | |||||
| 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. | 20…30 30…40 40…50 50…60 60…70 70…80 80…90 90…100 100…110 110…120 | // /// ////////// //////////////// /////////////////////////// ///////////////////////////////// ////////////////////////////////// /////////////////////// /////////// /// | 0,0123 0,0185 0,0617 0,0988 0,1667 0,2037 0,2099 0,1420 0,0679 0,0185 | ||
| Всьо-го | 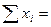 162 162
| 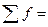 =1.0000
=1.0000
|
Для однієї вибірки даних можна побудувати багато гістограм з різною кількістю інтервалів. Всі ці гістограми матимуть подібний вигляд.
За формою гістограми можна прийняти робочу гіпотезу щодо належності даного розподілу до того чи іншого закону розподілу. Наприклад, для випадку, наведеного в табл. 2 – нормального розподілу. Але ця гіпотеза потребує подальшої математичної перевірки. Для визначення причин варіації параметра необхідно вміти аналізувати гістограми. Коректний аналіз можна зробити у випадку, коли вибірка перевищує 50 даних.
Нормальний розподіл має форму дзвона. Такий розподіл є характеристикою регулярного виробництва. Але все ж таки він може не задовольняти необхідним вимогам до продукту. У деяких випадках середнє значення не відповідає бажаному, в інших - дисперсія є дуже великою.
За законами, близькими до нормального, розподіляються поступові відмови, річні, добові та міжремонтні пробіги, простої автомобілів у технічному обслуговуванні та капітальному ремонті. Але напрацювання на раптові відмови та простої у поточних ремонтах розподіляються за законами, близькими до експоненціального.
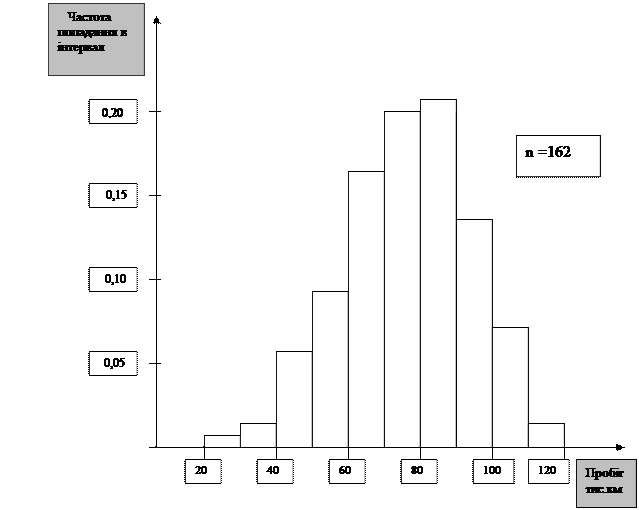
Рис. 12. Гістограма розподілу напрацювання на відмову деталі автомобіля.
Гістограми будуються здебільшого для аналізу значень виміряних параметрів, але може використовуватись і для отримання розрахункових значень. Завдяки простоті побудови та наочності гістограми використовуються в різних сферах .
Гістограми можуть використовуватись для вирішення таких задач:
· аналіз часу знаходження в СТО, супермаркеті, перукарні, майстерні, лікарні, банку, тощо;
· аналіз часу реагування групи обслуговування ( в будь-якому місці) від моменту отримання замовлення від клієнта;
· аналіз часу обробки рекламації від моменту її отримання, тощо;
· аналіз терміну виконання замовлення ( за контрольний норматив береться термін згідно укладеного договору);
· аналіз значень показників якості (розмір, маса, механічні характеристики, вихід продукції при контролі готової продукції, під час контролю перебігу процесу в різних сферах діяльності і т.п.);
· аналіз чистого часу операції, процесу, тощо;
· аналіз кількості бракованих виробів, кількості дефектів, кількості помилок, тощо.
Розрізняють такі модифікації форми гістограм:
1. Гістограма з двохсторонньою симетрією ( нормальний закон розподілу). Гістограма з таким розподілом зустрічається найчастіше. Вона вказує на стабільність процесу.
2. Гістограма витягнута вправо. Таку форму, із плавно витягнутою вправо основою, гістограма приймає у випадку, коли неможна мати значення параметру нижче певного визначеного.
3. Гістограма витягнута вліво. Таку форму, із плавно витягнутою вліво основою, гістограма приймає у випадку, коли неможна мати значення параметру вище певного визначеного.
4. Двохвершинна гістограма. Така гістограма містить дві вершини ( які найчастіше мають різну висоту ) із провалом між ними і відображає випадки об’єднання двох розподілів із різними середніми значеннями, наприклад, у випадку наявності різниці між двома станками, між двома операторами, між двома видами матеріалів і т.д. В цьому випадку можна зробити розсіювання по двом видам факторів, дослідити причини різниці та прийняти відповідні заходи для його відхилення.
5. Гістограма у формі обриву, у якої ніби обрізаний один кінець ( або обидва). Така гістограма представляє випадки, коли , наприклад, відібрані та виключені із партії всі вироби із параметрами нижче за контрольний норматив ( або вище контрольного нормативу, або перші та другі ). Після дослідження причин відхилення значень параметрів від норми та стабілізації процесу можна не відбирати вироби з параметрами, що відрізняються від нормальних.
6. Гістограма з нормально високим краєм ( у формі обриву). Така гістограма відображає випадки, коли, наприклад, потрібні виправлення параметра, що має відхилення від норми, або при спотворенні інформації тощо. Після стабілізації процесу, операції по виправленню невідповідності можуть бути зупинені.
7. Гістограма із окремим острівцем. Такою гістограмою показуються випадки, коли була допущена помилка при вимірюваннях, коли спостерігались відхилення від норми в ході процесу і т.д. По результатам аналізу гістограми роблять висновки про необхідність налаштування вимірювального приладу або негайного здійснення контролю параметрів процесу, та виконують відповідні заходи.
8. Гістограма з ”прогалиною” ( із ”вирваним зубом”). Таку гістограму отримують, коли ширина інтервалу не кратна одиниці вимірювання ( не виражається цілим числом у вибраній одиниці вимірювання), коли оператор помиляється у підрахунку показань шкали тощо.
9. Гістограма, що не має високої центральної частини. Таку гістограму отримують у випадках, коли об’єднуються декілька розподілів, в яких середні значення мають невелику різницю між собою. Аналіз такоїгістограми доцільно проводити, використовуючи метод розшарування.
У випадках, коли відомі допустимі відхилення розміру від номіналу (допуски), відмічають прямими лініями верхню та нижню границю допуску (встановлюють контрольні нормативи) для порівняння з ними розподілу, вираженого гістограмою. При цьому наглядно видно чи попадає гістограма в інтервал між контрольними нормативами.
Під час порівняння гістограми з допусками або з запланованими значеннями можуть мати місце такі випадки, а саме:
1. Середнє значення 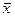 розподілу знаходиться посередині між контрольними нормативами, розсіювання не виходить за межі норми. Найбільш бажане положення, коли ширина між контрольними нормативами приблизно у вісім разів більше стандартного відхилення s.
розподілу знаходиться посередині між контрольними нормативами, розсіювання не виходить за межі норми. Найбільш бажане положення, коли ширина між контрольними нормативами приблизно у вісім разів більше стандартного відхилення s.
2. Гістограма повністю входить в інтервал, обмежений контрольними нормативами, але розсіювання значень велике. Межі гістограми знаходяться на границях допуску (ширина допуску в 5-6 разів більша стандартного відхилення s). При цьому існує можливість появи браку, необхідні заходи для зменшення розсіювання.
3. Середнє значення 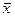 розподілу знаходиться посередині між контрольними нормативами, розсіювання також знаходиться в межах допуску, однак межі гістограми трохи не доходять до контрольних нормативів (ширина розподілу більш ніж в 10 разів перевищує стандартне відхилення s). Гарантія від появи браку. Якщо звузити ширину допуску, тобто зробити суворим стандарт на вироби, продукцію, тоді можна підвищити потужність виробництва та ефективність з точки зору збуту. Якщо трохи збільшити розсіювання, тобто зробити менш строгими стандарти на технологічні операції та норми на сировину (вхідні параметри), матеріали та комплектуючі, тоді можна підвищити продуктивність та знизити вартість вихідних матеріалів та комплектуючих.
розподілу знаходиться посередині між контрольними нормативами, розсіювання також знаходиться в межах допуску, однак межі гістограми трохи не доходять до контрольних нормативів (ширина розподілу більш ніж в 10 разів перевищує стандартне відхилення s). Гарантія від появи браку. Якщо звузити ширину допуску, тобто зробити суворим стандарт на вироби, продукцію, тоді можна підвищити потужність виробництва та ефективність з точки зору збуту. Якщо трохи збільшити розсіювання, тобто зробити менш строгими стандарти на технологічні операції та норми на сировину (вхідні параметри), матеріали та комплектуючі, тоді можна підвищити продуктивність та знизити вартість вихідних матеріалів та комплектуючих.
4. Розсіювання невелике у порівнянні із шириною норми, але із-за великого зміщення середнього значення  в сторону нижньої границі норми з’являється брак. При цьому необхідні заходи, які б сприяли переміщенню середнього значення до середньої точки між контрольними нормативами.
в сторону нижньої границі норми з’являється брак. При цьому необхідні заходи, які б сприяли переміщенню середнього значення до середньої точки між контрольними нормативами.
5. Середнє значення 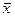 знаходиться посередині між контрольними нормативами, але із-за великого розсіювання межі гістограми виходять за межі допуску, тобто з’являється брак. Необхідні заходи по зменшенню розсіювання.
знаходиться посередині між контрольними нормативами, але із-за великого розсіювання межі гістограми виходять за межі допуску, тобто з’являється брак. Необхідні заходи по зменшенню розсіювання.
6. Середнє значення зміщено відносно центра допуску, розсіювання велике, з’являється брак. Необхідні заходи по переміщенню середнього значення до середньої точки між контрольними нормативами та зменшення розсіювання.
Таким чином, порівняння виду розподілу гістограми із допуском або запланованими значеннями дає важливу інформацію для управління процесом. Оскільки при цьому необхідно оперувати середнім значенням 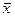 та стандартним відхиленням s, тому необхідно вміти їх вираховувати.
та стандартним відхиленням s, тому необхідно вміти їх вираховувати.
Розглянемо ще один приклад побудови гістограми.
На підприємстві за певний проміжок часу зібрані дані про розмір зовнішнього діаметра валу, який виготовляється відповідно до креслення. Результати замірів систематизовані та представлені в табл. 3. При цьому найбільше( Xmax ) та найменше( Xmin )значення відповідно: Xmax= 2.5433мм ,
Xmin = 2.5010 мм .
Таблиця 3.
Результати вимірювань зовнішнього діаметра валу
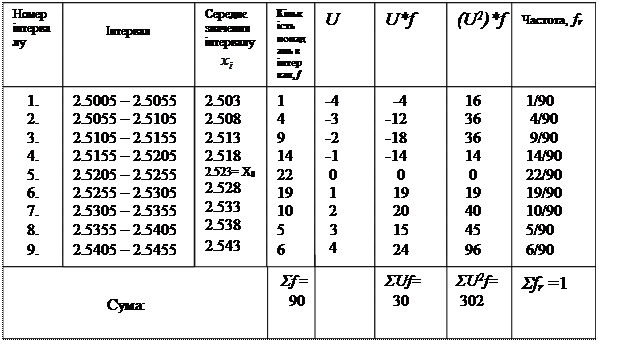
Послідовність побудови та аналізу гістограми наступна:
1) Обирають параметри виробу для контролю. Здійснюють вимірювання. Систематизують дані, що зібрані за певний проміжок часу. Кількість даних повинно бути не менше 30-50 , оптимальна кількість – 100. Якщо їх буде більше 300, затрати часу на їх обробку будуть великими. Виміряні значення вписують у відповідний контрольний лист реєстрації.
2) Серед виміряних значень знаходятьнайбільше 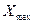 та найменше
та найменше 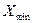 значення вимірюваного параметру.
значення вимірюваного параметру.
3)Визначають ширину розподілу R (розмах варіації) відповідно до (1)

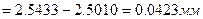
4)Визначають кількість інтервалів. Наприклад, при кількості даних 30-50 кількість інтервалів буде становити близько 5-7, при числу даних 50-100 – 6-10, при 100-200 – 8-15
 , (18)
, (18)
де: t – кількість інтервалів; n = 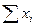 –кількість даних.
–кількість даних.
5)Визначають ширину інтервалу (h)
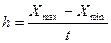 . (19)
. (19)
Отримане значення округлюють
 мм.
мм.
6)Визначають граничні значення інтервалів. Спочатку підраховують найменше граничне значення першого інтервалу
X1 min. = Xmin - 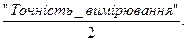 . (20)
. (20)
А саме:
X1min.= Xmin - 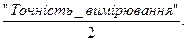 = 2.5010 мм –
= 2.5010 мм – 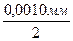 = 2.5005мм.
= 2.5005мм.
Найбільше граничне значення першого інтервалу становить
X1 max = X1 min + h . (21)
Згідно (21)
X1 max = X1 min + h = 2.5005 + 0,0050 =2.5055мм.
Граничні значення решти інтервалів визначають за формулами
Xi min = Xi-1 min + h; (22)
Xi max= Xi-1 max + h; (23)
Xi max= Xi min + h. (24)
Знаходимо, що перший інтервал становить [2.5005мм ; 2.5055мм]. Аналогічно прибавляючи 0.0050мм до 2.5055мм, отримуємо другий інтервал [2.5055; 2.5105] мм і т.д. Останній інтервал становить: [2.5405;2.5455 ] мм, в який входить найбільше виміряне значення зовнішнього діаметру деталі
Xmax = 2.5433мм.
7) Центральне значення і–го інтервалу визначають за формулою
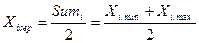 . (25)
. (25)
де X і сер- центральне значення і – го інтервалу;
Sum і – сума граничних значень і-го інтервалу;
Xi max – верхнє граничне значення і –го інтервалу;
Xi min – нижнє граничне значення і – го інтервалу.
Центральне значення першого інтервалу обчислюємо за формулою
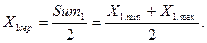 (26)
(26)
Згідно (26) 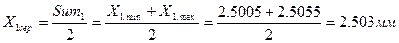 .
.
Центральні значення решти інтервалів обчислюють додаванням ширини інтервалу ( h) до центральних значень попередніх інтервалів
 (27)
(27)
8) Частоти попадання виміряних значень параметру у відповідний інтервал (табл. 3) визначають як відношення кількості випадків попадання в інтервал до загальної кількості випадків.
9) Для побудови гістограм по осі абсцис відкладають межі інтервалів значень параметрів якості, по осі ординат – шкалу частот. Для кожного інтервалу будують прямокутник ( стовпець ) із основою, що дорівнює ширині інтервалу, та висотою, яка пропорційна частоті попадання даних в цей інтервал (рис.13).
10) Обчислюють середнє значення ознаки 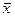 та стандартне відхилення s (табл. 3). Приймають U=0 для інтервалу, якому відповідає максимальне значення частоти попадання f = 22 (рядок 5, табл. 3). Від цього значення U=0 вгору та вниз записують для кожного рядка значення U відповідно зменшене та збільшене на 1 від попереднього :U= -1, -2, -3, ..., та U=+1,+ 2, +3,...і т.п.. Середнє значення інтервалу, для якого U=0, позначають через
та стандартне відхилення s (табл. 3). Приймають U=0 для інтервалу, якому відповідає максимальне значення частоти попадання f = 22 (рядок 5, табл. 3). Від цього значення U=0 вгору та вниз записують для кожного рядка значення U відповідно зменшене та збільшене на 1 від попереднього :U= -1, -2, -3, ..., та U=+1,+ 2, +3,...і т.п.. Середнє значення інтервалу, для якого U=0, позначають через 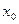 , ширину інтервалу – через h. Підраховують значення рядків в стовпцях:
, ширину інтервалу – через h. Підраховують значення рядків в стовпцях: 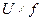 ,
, 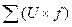 ,
, 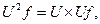
 . Далі визначають
. Далі визначають 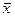 згідно формули:
згідно формули:
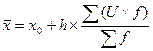 . (28)
. (28)
Наносять на гістограму лінію, що відповідає 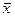 ( рис.13).
( рис.13).
Згідно (28)
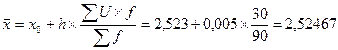 мм.
мм.
Стандартне відхилення визначимо за формулою
 =0,005
=0,005 
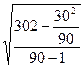 =0,00906 мм. (29)
=0,00906 мм. (29)

Рис. 13. Гістограма розсіювання значень зовнішнього діаметра валу.
1 – нижня границя допуску: SL = 2,495мм;
2 – верхня границя допуску: SU = 2,555мм.
На побудованій гістограмі проводять лінії, перпендикулярні осі абсцис, що відповідають значенням середньому значенню  та стандартному відхиленню S, а також верхній та нижній границям допуску та потрійному стандартному відхиленню
та стандартному відхиленню S, а також верхній та нижній границям допуску та потрійному стандартному відхиленню 
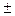 3S.
3S.
11)Визначають показник потужності процесу (коефіцієнт запасу точності технологічного процесу, індекс відтворюваності процесу ) 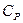 , за допомогою якого роблять висновок про стан розподілу по відношенню до допуску, дослідити можливість виробництва продукції потрібної якості за допомогою даного технологічного процесу, тобто кількісно оцінити точність технологічного процесу.
, за допомогою якого роблять висновок про стан розподілу по відношенню до допуску, дослідити можливість виробництва продукції потрібної якості за допомогою даного технологічного процесу, тобто кількісно оцінити точність технологічного процесу.
У випадку, коли є верхня та нижня границі норми та гістограма розміщена між ними, показник потужності процесу 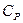 розраховується за формулою :
розраховується за формулою :
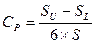 (30)
(30)
де: SU – верхня границя норми; SL - нижня границя норми;
S – стандартне відхилення.
Також, ступінь відхилення оцінюють за допомогою показника потужності процесу по відновленню відхилення ( 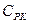 )
)
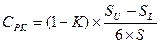 (31)
(31)
де: К – ступінь відхилення, визначається за формулою:
 (32)
(32)
У випадку, коли є одна границя норми показник потужності процесу 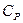 визначається за формулою
визначається за формулою
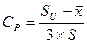 , (33)
, (33)
або  . (34)
. (34)
Пояснимо сказане вище на прикладі. Проведемо розрахунки для таких умов. Маємо : 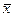 . = 2,52467 мм; S = 0,00906 мм;
. = 2,52467 мм; S = 0,00906 мм;
SL = 2,495мм; SU = 2,555мм.
Тоді отримуємо 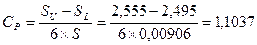
Ступінь відхилення К
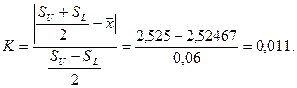
Показник потужності процесу по відновленню відхилення Срк :
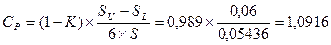
 .
.
Точність технологічного процесу оцінюють за такими критеріями:
1) Якщо 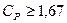 , тоді ширина інтервалу між контрольними нормативами не менше, ніж в десять раз перевищує стандартне відхилення S розсіювання параметрів виробу невелике, поява браку не передбачається. В цьому випадку доцільно зменшити клас вихідного матеріалу, комплектуючих ( сировини ) та спростити контроль процесу, що призведе до зниження собівартості продукції, трохи до звуження ширини інтервалу між нижньою та верхньою границями норми, покращення стратегії збуту продукції.
, тоді ширина інтервалу між контрольними нормативами не менше, ніж в десять раз перевищує стандартне відхилення S розсіювання параметрів виробу невелике, поява браку не передбачається. В цьому випадку доцільно зменшити клас вихідного матеріалу, комплектуючих ( сировини ) та спростити контроль процесу, що призведе до зниження собівартості продукції, трохи до звуження ширини інтервалу між нижньою та верхньою границями норми, покращення стратегії збуту продукції.
2) Якщо 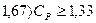 , тоді ширина інтервалу між контрольними нормативами у вісім – десять разів перевищує стандартне відхилення S. Це є ідеальний стан процесу.
, тоді ширина інтервалу між контрольними нормативами у вісім – десять разів перевищує стандартне відхилення S. Це є ідеальний стан процесу.
3) Якщо 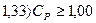 , тоді ширина інтервалу між контрольними нормативами в шість – вісім разів перевищує стандартне відхилення S. Коли
, тоді ширина інтервалу між контрольними нормативами в шість – вісім разів перевищує стандартне відхилення S. Коли 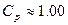 , тоді ймовірність появи браку складає 0.27 % ( табл. 1 ). В цьому випадку необхідно підсилити контроль процесу, провести аналіз факторів, що впливають на розсіювання, та заходи поліпшення стану процесу.
, тоді ймовірність появи браку складає 0.27 % ( табл. 1 ). В цьому випадку необхідно підсилити контроль процесу, провести аналіз факторів, що впливають на розсіювання, та заходи поліпшення стану процесу.
4) Якщо 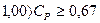 , тоді ширина інтервалу між нижньою та верхньою границею норми в чотири – шість разів перевищує стандартне відхилення S . Коли показник
, тоді ширина інтервалу між нижньою та верхньою границею норми в чотири – шість разів перевищує стандартне відхилення S . Коли показник 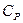 наближається до 0.67 (
наближається до 0.67 ( 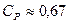 ), тоді ймовірність появи браку складає 4.56 % (табл.1). Це означає, що контроль процесу незадовільний. В такому випадку необхідно налагодити суцільний контроль процесу та випускаючих виробів (продукції) з метою недопускання браку. Необхіднопровести дослідження факторів, що впливають на розсіювання, та заходи поліпшення стану процесу.
), тоді ймовірність появи браку складає 4.56 % (табл.1). Це означає, що контроль процесу незадовільний. В такому випадку необхідно налагодити суцільний контроль процесу та випускаючих виробів (продукції) з метою недопускання браку. Необхіднопровести дослідження факторів, що впливають на розсіювання, та заходи поліпшення стану процесу.
5) Якщо 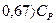 , тоді ширина інтервалу між нижньою та верхньою границями норми не перевищує 4S. Відсоток браку перевищує 4.56 %. Такий процес неконтрольований. Необхідно провести суцільний контроль продукції, щоб попередити випуск бракованих виробів, та заходи для підвищення якості. Вияснити причини появи браку. Іноді необхідно знову провести вивчення потреб споживачів ( клієнтів ) і переглянути норми.
, тоді ширина інтервалу між нижньою та верхньою границями норми не перевищує 4S. Відсоток браку перевищує 4.56 %. Такий процес неконтрольований. Необхідно провести суцільний контроль продукції, щоб попередити випуск бракованих виробів, та заходи для підвищення якості. Вияснити причини появи браку. Іноді необхідно знову провести вивчення потреб споживачів ( клієнтів ) і переглянути норми.
Аналіз гістограми та стану процесу за допомогою показника 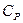 доцільно проводити в комбінації із застосуванням контрольних карт ( див. розділ 6.3 ).
доцільно проводити в комбінації із застосуванням контрольних карт ( див. розділ 6.3 ).
Якщо на гістограмі провести криву розподілу даних по частоті, верхнє та нижнє граничні значення допуску, можна визначити вид розподілу гістограми та співвідношення значень контрольних нормативів. Аналіз гістограми дозволяє зробити висновок про стан процесу. Якщо умови контролю процесу чи зміни в часі незрозумілі, тоді в комбінації з гістограмою використовують інші інструменти управління якістю. Отримана в результаті аналізу гістограми інформація використовується для побудови та дослідження причинно-наслідкової діаграми для підвищення обґрунтованості заходів поліпшення якості процесу.
Завдання для самостійної роботи.
На підприємстві контролюється товщина деталі автомобіля. Цей параметр є важливим для споживача. Результати спостережень систематизовані та представлені у вигляді таблиці 4 та гістограми (рис.14). Використовуючи отримані дані, провести розрахунки для визначення статистичних показників вимірювання варіації ознак якості деталі автомобіля.
Таблиця 4.
Результати вимірювання товщини деталі


Рис.14. Гістограма розсіювання товщини деталі автомобіля
1 – нижнє граничне значення допуску; 2 – верхнє граничне значення допуску .
6.3. Контрольні карти
Контрольна карта – це графічний засіб оцінки певної ознаки якості, виміряні значення якої наносяться на графік відповідно до порядку отримання їх у часі.
Принцип побудови і використання контрольних карт полягає внаступному.
Розглянемо найбільш загальний довільний виробничий процес, який має місце в будь-якому комерційному підприємстві, до яких відносяться і автосервісні підприємства (станції технічного обслуговування автомобілів - СТОА), і результатом якого є певна сума виручки, наприклад, за день.
Керівник підприємства для контролю за результатами діяльності своєї фірми будує графік змін денної виручки в часі (рис. 15). При цьому на горизонтальній осі позначаються дні, а по вертикальній відкладається величина денної виручки. Такі графіки називають картами поточних значень контрольованого параметру – у даному випадку денної виручки.
В кінці декількох тижнів спостережень, на протязі яких не було якихось особливих змін виручки, керівник підрахував середнє значення денної виручки і позначив його на графіку у вигляді горизонтальної лінії. При цьому стало помітно, що точки спостережень розташовувались відносно рівномірно вище і нижче середньої лінії.
Продовжуючи спостереження, через деякий час керівник зареєстрував стабільне зниження денної виручки на протязі дев’яти днів поспіль, що на графіку контролю мало вигляд розташування дев’яти послідовних точок нижче середньої лінії.
Це явище здалося йому аномальним і навело на думку, що звичайний процес роботи підприємства був деформований наявністю якогось спеціального чинника.
Після детального вивчення ситуації виявилось, що один з автомеханіків організував у себе в гаражі власну майстерню і домовлявся з клієнтами щодо виконання їх замовлень не на СТОА, де він працював, а в себе за меншу ціну. При цьому, не сплачуючи податків, він отримував більше, ніж за цю ж роботу на СТОА. Клієнту ж також це обходилось значно дешевше, ніж на автосервісному підприємстві. Після звільнення цього працівника і заміни його іншим, ситуація була взята під контроль і процес стабілізувався, що знайшло свої відображення на карті контролю поточних значень денної виручки.
Контрольні карти вперше були запропоновані відомим американським фахівцев в галузі якості Уолтером Шухартом [2,8] тому носять його назву.
На контрольних картах Шухарта наносять три горизонтальні лінії: центральну лінію, а також верхню та нижню контрольні границі.
Центральна лінія відображає деяке усереднення поточних значень контрольованого параметру. Звичайно це середнє арифметичне, але може бути і медіанним значенням [7].
Верхня та нижня контрольні границі розташовані на відстані ± 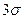 ,де
,де 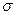 є середньоквадратичним відхиленням. Раніше було показано, що за таких умов при нормальному розподілі випадкової величини
є середньоквадратичним відхиленням. Раніше було показано, що за таких умов при нормальному розподілі випадкової величини 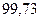 % її поточних значень будуть знаходитись між нижньою та верхньою контрольними границями. Тобто тільки приблизно в трьох випадках з тисячі контрольована величина вийде за межі цих контрольних границь.
% її поточних значень будуть знаходитись між нижньою та верхньою контрольними границями. Тобто тільки приблизно в трьох випадках з тисячі контрольована величина вийде за межі цих контрольних границь.
Правило Шухарта полягає в тому [2,8], що спеціальний чинник, наявність якого робить виробничу систему нестабільною, є присутнім тоді, коли значення контрольованого параметру виходить за межі будь-якої з контрольних границь. Інші дослідники внесли свої доповнення в методологію використання контрольних карт для виявлення присутності спеціального чинника. Так згідно з критеріями Нельсона сигналом наявності спеціального чинника також є розташування 9 точок поспіль з однієї сторони центральної лінії, або безперервне збільшення чи зменшення контрольованої величини в 6 послідовних точках. Описані вище ситуації показані на рис.15.
Дата добавления: 2014-12-05; просмотров: 1879;
