Формулы алгебры логики
Формулами алгебры логикиназываются выражения, полученные из переменных x, y,… посредством применения логических операций: отрицания, конъюнкции, дизъюнкции, импликации и эквиваленции, а также сами переменные, принимающие значения истинности высказываний x, y,….
Если в формулу алгебры логики вместо переменных x, y,… подставить конкретные высказывания, то получится высказывание, имеющее логическое значение «1» или «0».
Пример.
Высказывание x: «Волга впадает в Каспийское море» – истинное (x = 1),
высказывание y: «Число 16 кратно 3» – ложное (y = 0),
тогда формула А = x Ú y будет иметь логическое значение «1»: А = 1 (см. таблицу истинности для х Ú y).
На основе таблиц истинности основных логических операций можно составлять таблицы истинности для различных формул алгебры логики.
Две формулы алгебры логики называются равносильнымиили эквивалентными, если они принимают одинаковые логические значения на любом наборе значений входящих в формулы переменных (элементарных высказываний). Равносильность формул будем обозначать знаком «º».
Равносильность логических формул можно установить при помощи их таблиц истинности.
Пример. С помощью таблиц истинности проверить, являются ли равносильными формулы  и
и  .
.
Решение. Составим таблицы истинности для каждой из формул А и В.
| x | y | 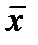
| 
| 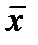 Ù Ù 
| 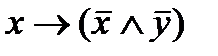
|
| x | y | 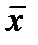
| x Ú y | 
| 
|
Ответ: данные формулы являются равносильными.
Другой способ доказательства равносильности логических формул – их упрощение с использованием равносильных преобразований.
Примеры равносильных преобразований:
1) x ® y º 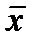 Ú y; 3)
Ú y; 3) 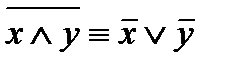 ;
;
2) x « y º (x ® y) Ù (y ® x); 4) 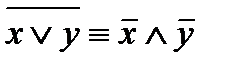 .
.
Для упрощения записи формул принят ряд соглашений. Скобки можно опускать, придерживаясь следующего порядка действий: Сначала выполняем действия в скобках, затем отрицание, затем выполняется конъюнкция. Если над формулой стоит знак отрицания, то скобки тоже опускаются.
Пример 1. Упростить логическую формулу:  .
.
Решение. Используем основные равносильности.

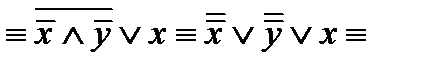
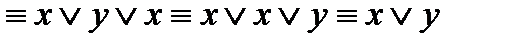 .
.
Ответ: x Ú y.
Пример 2. Являются ли эквивалентными следующие высказывания:
Решение.
Составим таблицы истинности для каждого высказывания.
| x | y | z | y|z | 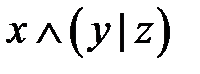
| 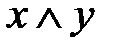
| 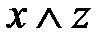
| 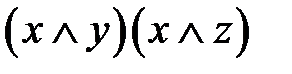
|
Значения x и y в пятом и восьмом столбцах не совпадают.
Вывод: данные высказывания не являются эквивалентными.
Дата добавления: 2014-12-05; просмотров: 1586;
