Основные логические операции над высказываниями.
Отрицанием высказывания х называется высказывание, которое истинно тогда и только тогда, когда высказывание х ложно. Отрицание обозначается 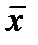 или -х (читается: «не х»).
или -х (читается: «не х»).
Логические операции можно задавать при помощи таблиц истинности, показывающих соответствие значений истинности высказываний. Для высказываний x и 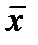 эта таблица имеет вид:
эта таблица имеет вид:
| х | 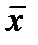
|
Конъюнкцией двух высказываний х и y называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания х и y. Конъюнкция обозначается: х Ù y,или х & y (читается: «х и y»). Таблица истинности для х Ù y имеет вид:
| х | y | х Ù y |
Дизъюнкцией двух высказываний х и y называется высказывание, ложное тогда и только тогда, когда оба высказывания х и y ложны. Дизъюнкция обозначается х Ú y (или x+y)(читается: «х или y»). Таблица истинности для х Ú y имеет вид:
| х | y | х Ú y |
Импликацией двух высказываний х и y называется высказывание, ложное тогда и только тогда, когда высказывание х истинно, а y – ложно. Импликация обозначается: х ® y (читается: «х влечет y» или «из х следует y»). Высказывание х называется посылкой импликации, а высказывание y – следствием. Таблица истинности для х ® y имеет вид:
| х | y | х ® y |
Эквиваленцией (эквивалентностью) двух высказываний х и y называется высказывание, истинное тогда и только тогда, когда истинности высказываний х и y совпадают. Эквиваленция обозначается: х « y, или х ~ y (читается: «х эквивалентно y» или «х тогда и только тогда, когда y»). Таблица истинности для х « y имеет вид:
| х | y | х « y |
Сложением по модулю два (альтернативной дизъюнкцией, логи́ческим сложе́нием, исключа́ющим «ИЛИ», строгой дизъюнкцией) двух высказываний х и y называется высказывание, истинное тогда и только тогда, когда оба высказывания х и y принимают разные значения. Дизъюнкция обозначается хÅy (читается: «или х, или y»). Таблица истинности для хÅy имеет вид:
| х | y | хÅy |
| 0 | 0 | 0 |
Стрелка Пирса – этоотрицание дизъюнкции. Стрелка Пирса обозначается X ↓ Y. Читается «ни X, ни Y». Введена в рассмотрение Чарльзом Пирсом (Сharles Peirce) в 1880—1881 г.г. Таблица истинности для стрелки Пирса имеет вид:
| х | y | х ↓ y |
Штрих Шеффера – это отрицание конъюнкции. Введена в рассмотрение Генри Шеффером в 1913 г. (в отдельных источниках именуется как Пунктир Чулкова). Штрих Шеффера обозначается x|y , задаётся следующей таблицей истинности:
| х | y | x|y |
Дата добавления: 2014-12-05; просмотров: 1992;
