Релейно-контактные схемы
Релейно-контактной схемой (РКС) или переключательной схемой называется схематическое изображение устройства, состоящего из следующих элементов:
1) переключателей (контактов, реле, ламп и др.);
2) соединительных проводников;
3) входов-выходов (полюсов РКС).
Рассмотрим простейшую РКС, содержащую один переключатель Р. Если переключателю Р поставить в соответствие высказывание х: «Переключатель Р замкнут», то истинному значению х (х = 1) будет соответствовать замкнутое состояние переключателя, при котором РКС проводит ток, т.е. импульс, поступающий на вход, может быть снят на выходе. Значению х = 0 будет соответствовать разомкнутое состояние РКС (ток не проводится). Каждой РКС, состоящей из нескольких переключателей, можно поставить в соответствие высказывание, выраженное некоторой формулой А, таким образом, что истинному значению формулы (А = 1) будет соответствовать замкнутое состояние РКС, а значению А = 0 – разомкнутое состояние. Примеры таких соответствий приведены в таблице.
Простейшие РКС и соответствующие им формулы логики.
| РКС | Формула | Значения |
Переключатель х:
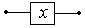
| Простейшее высказывание: х | х = 1, если переключатель замкнут; х = 0, если переключатель разомкнут |
Переключатель 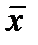
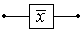
| Отрицание простейшего высказывания: 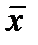
| 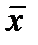 = 0, если переключатель замкнут; = 0, если переключатель замкнут;
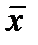 = 1, если переключатель разомкнут = 1, если переключатель разомкнут
|
Последовательное соединение:
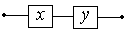 (схема замкнута, когда
оба переключателя замкнуты)
(схема замкнута, когда
оба переключателя замкнуты)
| Конъюнкция высказываний: x Ù y | 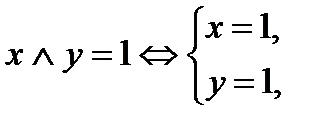
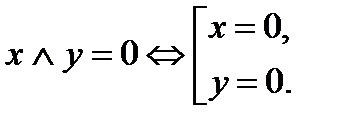
|
Параллельное соединение:
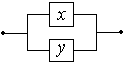 (схема разомкнута, когда
оба переключателя разомкнуты)
(схема разомкнута, когда
оба переключателя разомкнуты)
| Дизъюнкция высказываний: x Ú y | 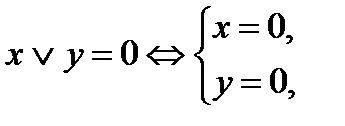
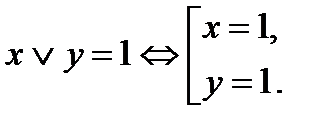
|
Схема, которая всегда разомкнута
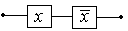
| x Ù 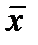
| x Ù 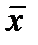 º 0 º 0
|
Схема, которая всегда замкнута
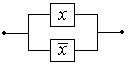
| x Ú 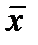
| x Ú 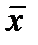 º 1 º 1
|
Из простейших РКС путем их последовательного и параллельного соединения могут быть построены более сложные переключательные схемы.
Доказано, что любая формула алгебры логики может быть преобразована к виду, содержащему только операции отрицания, конъюнкции и дизъюнкции. Это позволяет изображать логические формулы при помощи РКС, а РКС задавать формулами.
Например, согласно формулам основных равносильностей
x ® y º 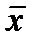 Ú y и x « y º (x ® y) Ù (y ® x),
Ú y и x « y º (x ® y) Ù (y ® x),
следовательно, логическим операциям импликации и эквиваленции соответствуют РКС, изображенные рис. 1.
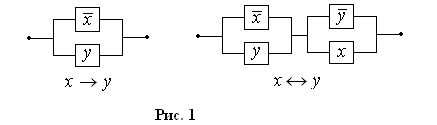
Используя равносильные преобразования логической формулы, соответствующей некоторой РКС, можно упростить РКС, т.е. привести ее к виду, содержащему меньшее число переключателей.
1.  Образец решения.
Образец решения.
Пример.
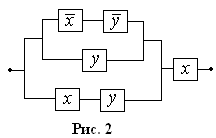
Упростить РКС, изображенную на рис. 2.
Решение. Запишем
соответствующую РКС формулу, используя таблицу простейших РКС и соответствующих им формул логики:
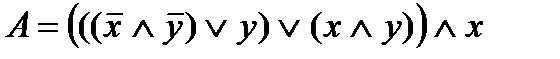 .
.
Упростим формулу, используя основные равносильности:
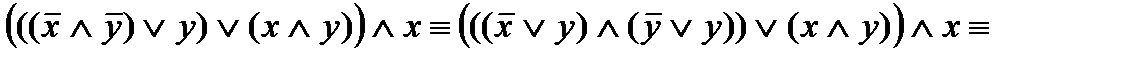
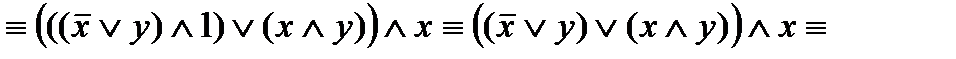
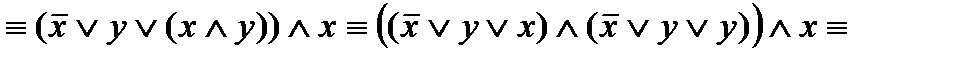
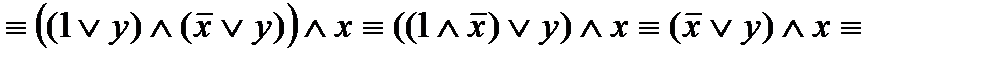
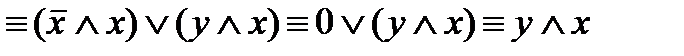 .
.
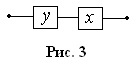
Таким образом, 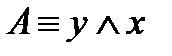 . Построим РКС, соответствующую упрощенной формуле (рис. 3).
. Построим РКС, соответствующую упрощенной формуле (рис. 3).
Содержание работы
Задание 1. Используя понятия перестановок, размещений и сочетаний, решите задачи:
1.1. Сколькими способами в бригаде, состоящей из пяти рабочих, можно распределить три путевки: в дом отдыха, в санаторий и на турбазу?
1.2. Группа из 28 учащихся обменялась фотокарточками. Сколько всего было роздано фотокарточек?
1.3. В поезде 6 вагонов. Сколькими способами можно распределить по вагонам 6 проводников, если за каждым вагоном закрепляется один проводник?
1.4. Сколькими способами 7 различных путевок можно распределить в бригаде из 7 рабочих?
1.5. Сколько шестизначных чисел, делящихся на 25, можно составить из цифр 1, 2, 3, 4, 5, 6, если все цифры в числах различны?
Задание 2. Используя понятия перестановок, размещений и сочетаний, решите задачи:
2.1. На шесть сотрудников выделены три одинаковые путевки в дом отдыха. Сколькими способами их можно распределить?
2.2. Сколькими способами можно увезти со склада 10 ящиков на двух автомашинах, если на каждую автомашину грузят по 5 ящиков?
2.3. В стройотряде 15 студентов. Сколькими способами их можно разбить на три бригады численностью 3, 7 и 5 человек?
2.4. На погранзаставе 40 рядовых и 8 офицеров. Сколькими способами из них можно составить наряд по охране границы, если он состоит из двух офицеров и четырех рядовых?
2.5. Из 12 красных и 8 белых гвоздик надо составить букет так, чтобы в нем были 3 красные и 2 белые гвоздики. Сколькими способами можно составить такой букет?
Задание 3. Укажите, высказывание истинно или ложно:
3.1. 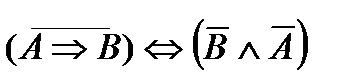
3.2. 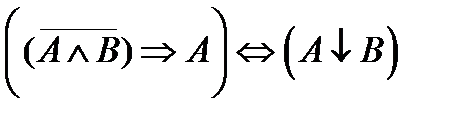
3.3. 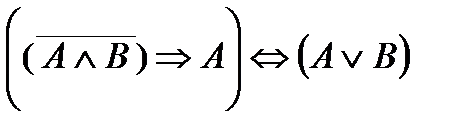
3.4. 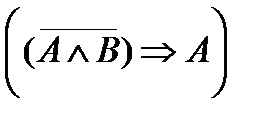
3.5. 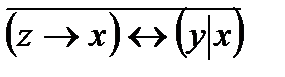
Задание 4. Являются ли эквивалентными следующие высказывания:
4.1. 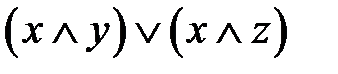 и
и 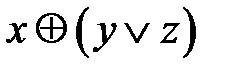
4.2. 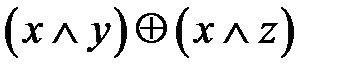 и
и 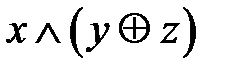
4.3. 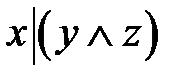 и
и 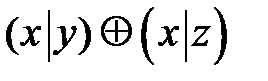
4.4. 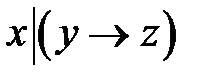 и
и 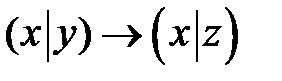
4.5. 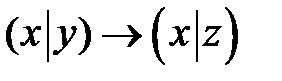
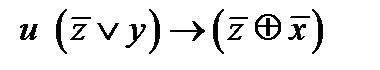
Задание 5. Определить значение истинности высказываний:
5.1. «Число 6 делится на 2 и число 6 делится на 3».
5.2. «На уроке математики старшеклассники отвечали на вопросы учителя и писали самостоятельную работу».
5.3. «Число делится на 3 тогда и только тогда, когда сумма цифр числа делится на 3».
5.4. «Число 376 четное и трехзначное».
5.5. «Если сумма цифр числа делится на 3, то число делится на 3».
Задание 6.Для множеств А и В:
6.1.
1. Найти 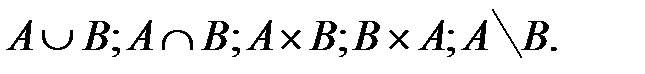
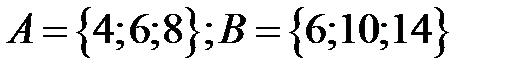
2. Доказать равенство и записать двойственное ему: 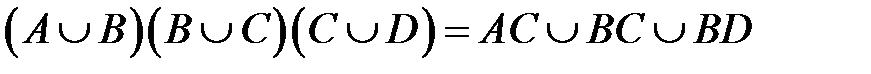
6.2.
1. Найти 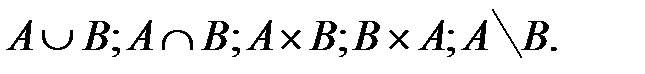
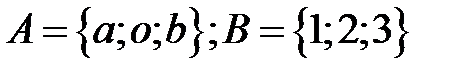
2. Доказать равенство и записать двойственное ему: 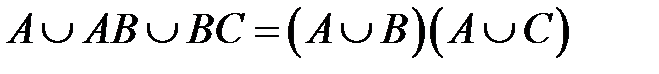

6.3.
1. Найти 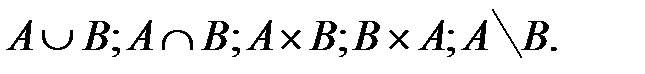
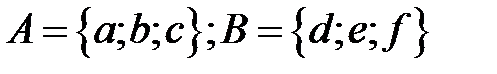
2. Доказать равенство и записать двойственное ему: 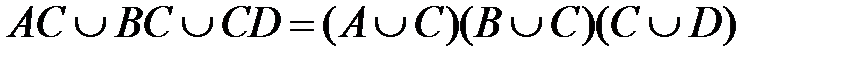
6.4.
1. Найти 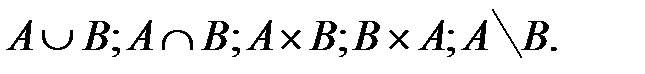
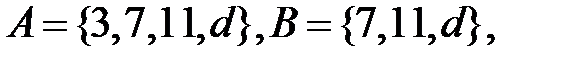
2. Доказать равенство и записать двойственное ему: 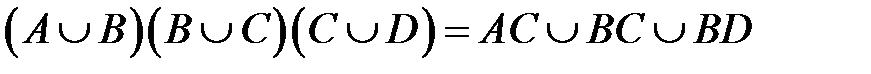
6.5.
1. Найти 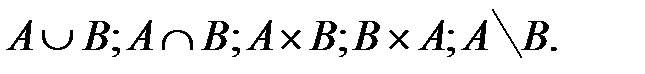
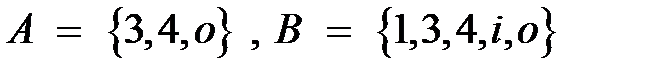
2. Доказать равенство и записать двойственное ему: 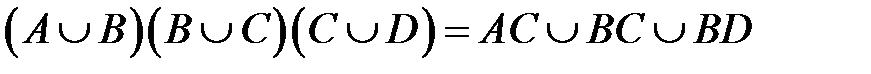
Вопросы для самоконтроля
- Какой раздел математики называют комбинаторикой?
- Что называется перестановками событий?
- Что называется размещениями событий?
- Что называется сочетаниями событий?
- Что понимают в математической логике под высказыванием?
- Какие действия выполняются над высказываниями?
- Что называют алгеброй Буля?
- Перечислите законы алгебры Буля.
- Что понимают под множеством?
- Способы задания множеств.
- Какое множество называют пустым? Универсальным?
- Перечислите действия над множествами.
- Сформулируйте законы действий над множествами.
Дата добавления: 2014-12-05; просмотров: 10962;
