Теорема Кука
1. Определение класса NP. Выше был принят тезис, согласно которому “эффективный алгоритм” - это алгоритм полиномиальной сложности. Однако имеется значительно число задач, для которых не найдено эффективного алгоритма. Следует различать следующие аспекты этого явления.
1) Не удалось найти эффективного алгоритма;
2) Эффективного алгоритма не существует;
3) Не удалось найти эффективного алгоритма, но существование такого алгоритма влечет за собой существование эффективного алгоритма для многих общепринято трудных задач.
Высказывание 2) удается получить только для очень узких классов разрешающих алгоритмов. Для практически приемлемых классов алгоритмов таких результатов нет. Высказывания 3) связаны с новой математической теорией, основанной на понятии NP-полноты и полиномиальной сводимости. Для удобства изложения данная теория строится для задач распознавания, т.е. задач, имеющих ответом “да” и “нет”. Введем класс NP задач распознавания, который включает в себя класс задач Р.
Задача распознавания П принадлежит классу NP если и только если она может быть решена на некоторой недетерминированной машине Тьюринга с полиномиальной сложностью.
Для задачи из класса NP требуется, чтобы в том случае, когда индивидуальная задача x имеет ответ “да”, то существует краткое (т.е. с длиной, ограниченной полиномом от размера x) удостоверение для x, справедливость которого можно было бы проверить за полиномиальное время (именно это удостоверение или соответствующее решение находит угадывающий модуль недетерминированной машины Тьюринга).
Пример. Задача КЛИКА. Даны граф G(V,E) и целое число k. Требуется узнать, существует ли в графе G клика, т.е. полный граф на подмножестве множества V, имеющий k вершин.
Не известно, справедливо ли КЛИКА Î P. Непосредственный перебор требует 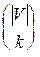 подмножеств из V проверять на связность. Это число экспоненциально. Однако верно, что КЛИКА Î NP.
подмножеств из V проверять на связность. Это число экспоненциально. Однако верно, что КЛИКА Î NP.
Действительно, пусть дана индивидуальная задача КЛИКА с ответом “да”, т.е. граф G(V,E) и целое число k, такие, что в графе G имеется клика размера k. Тогда для этой задачи имеется короткое удостоверение, а именно - список вершин, составляющих клику (этот список угадывающий модуль на первой стадии работы НТ записывает на ленту в ячейки с номерами -1,-2,...). Справедливость этого удостоверения можно проверить эффективно, т.к. нужно проверить, что в этом списке точно k вершин, и все эти вершины связаны ребрами из Е (это проводится на второй стадии работы НТ - стадии решения).
Формализуем эти идеи. Пусть А - фиксированный конечный алфавит и * - выделенный символ в А, который используется как знак-разграничитель. Если x - слово в алфавите А, то через  обозначим его длину. Будем говорить, что задача распознавания П входит в класс NP, если существует полином p(n) и алгоритм М (алгоритм проверки удостоверения), такие, что выполнено свойство: строка x является индивидуальной задачей задачи П с ответом “да” Û существует строка c(x) (удостоверение) в алфавите А, что ½c(x)½ < p(½x½) и алгоритм М, получая вход x*c(x) , приходит к ответу “да” после не более p(½x½) шагов. Например, в задаче КЛИКА x представляет индивидуальную задачу (G,k) с ответом “да”, то удостоверением c(x) для x может быть список вершин подходящей клики. Алгоритм проверки удостоверения проверяет, действительно ли x представляет граф G и целое число k, действительно ли c(x) - множество вершин из V мощности k и для каждой пары вершин из c(x) существует ребро в G. В качестве полинома p(n) можно взять 2n2, n =½V½.
обозначим его длину. Будем говорить, что задача распознавания П входит в класс NP, если существует полином p(n) и алгоритм М (алгоритм проверки удостоверения), такие, что выполнено свойство: строка x является индивидуальной задачей задачи П с ответом “да” Û существует строка c(x) (удостоверение) в алфавите А, что ½c(x)½ < p(½x½) и алгоритм М, получая вход x*c(x) , приходит к ответу “да” после не более p(½x½) шагов. Например, в задаче КЛИКА x представляет индивидуальную задачу (G,k) с ответом “да”, то удостоверением c(x) для x может быть список вершин подходящей клики. Алгоритм проверки удостоверения проверяет, действительно ли x представляет граф G и целое число k, действительно ли c(x) - множество вершин из V мощности k и для каждой пары вершин из c(x) существует ребро в G. В качестве полинома p(n) можно взять 2n2, n =½V½.
ЗадачаВЫПОЛНИМОСТЬ (ВЫП).
Пусть X = {x1,...,xn} - множество булевых переменных. Если xi - переменная, то xi и 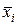 называется литералом над X. Очевидным образом определяется значение истинности литерала:
называется литералом над X. Очевидным образом определяется значение истинности литерала:
Литерал xi принимает значение 1 Û переменная xi = 1. Литерал 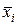 принимает значение 1 Û переменная xi = 0. Дизъюнкция D над X есть множество литералов над X.
принимает значение 1 Û переменная xi = 0. Дизъюнкция D над X есть множество литералов над X.
Дизъюнкция D принимает значение 1 Û существует набор значений переменных, при которых хотя бы один литерал из D принимает значение 1. Набор дизъюнкций С = {D1,...,Dm} выполним, если существует набор значений переменных, при котором все дизъюнкции принимают значение 1. В задаче ВЫПОЛНИМОСТЬ дано множество булевых переменных и набор дизъюнкций С. Требуется установить, существует ли набор значений переменных, выполняющий С. Другими словами, задача ВЫП есть задача распознавания для произвольной КНФ булевой функции, f(x1,...,xn) верно ли f(x1,...,xn) ¹ 0? Справедливо соотношение
ВЫП Î NP (3.1)
¨Действительно, если дано выполнимое множество дизъюнкций D1,...,Dm, содержащих булевы переменные x1,...,xn, то подходящим удостоверением может служить набор значений переменных - набор длины n из 0, 1. Алгоритм проверки удостоверения будет просто проверять, что D1,...,Dm - подмножества множества литералов из n переменных и что все дизъюнкции принимают значение 1 на данном наборе переменных. ¨
Важно подчеркнуть, что для установления принадлежности некоторой задачи классу NP не нужно объяснять, как эффективно вычислить удостоверение c(x) по входу x. Необходимо просто показать существование по крайней мере одной такой строки для каждого x.
Справедливо соотношение
P Í NP (3.2)
¨ Соотношение (3.2) означает, что любая эффективно решаемая задача позволяет строить краткие удостоверения. Пусть для задачи П существует полиномиальный алгоритм МП. Если x - индивидуальная задача задачи П с ответом “да”, то алгоритм МП, применимый к x, за полиномиальное число шагов выдаст ответ “да”. Запись работы алгоритма МП при входе x и есть подходящее удостоверение c(x). Действительно, для проверки c(x) достаточно проверить, что это правильное вычисление алгоритма МП, заметим, что по определению, c(x) полиномиально по длине. ¨
Класс NP представляет интерес с точки зрения практических приложений, поскольку он включает в себя многие важные в практическом отношении задачи из разных разделов дискретной математики. В частности, класс NP естественно появляется при изучении сложности комбинаторных задач оптимизации. Важной проблемой является установление того, верно ли Р = NP или Р - собственное подмножество NP ? Если Р ¹ NP, то задачи из NP\Р - примеры труднорешаемых задач, если Р = NP, то тогда многие задачи, известные своей трудностью, например КЛИКА, ВЫП - входили бы в Р, т.е. были бы эффективно решаемыми, что является маловероятным в силу приводимых ниже понятий и фактов.
Теорема 3.1. Если П Î NP, то существует такой полином p, что задача П может быть решена детерминированным алгоритмом с временной сложностью О(2p(n)), n - размер П.
¨ По определению существует полином q(n), что удостоверение c(x) индивидуальной задачи x имеет длину, не превосходящую q(n). Если k - мощность алфавита А, то число удостоверений не превосходит kq(n). (Считаем, что все удостоверения имеют длину q(n), в противном случае можно их подравнять). По условию, существует полином q1(n), ограничивающий время работы алгоритма МП, решающего задачу П по входу x*c(x). Теперь можно решить задачу детерминированным образом, перебирая для индивидуальной задачи x все входы x*c(x) и решая их полиномиальным алгоритмом. Временная сложность данного алгоритма q1(n)×kq(n). Ясно, что существует полином p(n), при котором общая сложность не превосходит О(2p(n)). ¨
2. Полиномиальная сводимость и NP-полнота. Пусть П1 и П2 - задачи распознавания. Будем говорить, что П1 сводится заполиномиальное время к П2 тогда и только тогда, когда существует полиномиальный алгоритм М1 для П1, использующий в качестве подпрограммы с единичной стоимостью алгоритм М2, решающий П2. Будем называть М1 полиномиальным сведением П1 к П2. Предположение “с единичной стоимостью” означает, что алгоритм М2 рассматривается как единый оператор, для выполнения которого требуется единица времени. Если П1 сводится за полиномиальное время к П2, то будем записывать П1 µ П2.
Теорема 3.2. Если П1 полиномиально сводится к П2 и существует полиномиальный алгоритм для П2, то существует полиномиальный алгоритм для П1.
¨ Пусть p1(n) и p2(n) - полиномы, ограничивающие сложность алгоритмов М1 (в предположении, что вызов М2 имеет единичную стоимость) и М2. Тогда действительная сложность алгоритма М1 для входа размера n при условии, что каждый вызов М2 стоит столько, сколько требуется времени для выполнения M2 с текущими параметрами, ограничена величиной
p(n) = p1(n) ×p2(p1(n)).
Действительно, в худшем случае M1 будет состоять из непрерывных вызовов M2 , каждый раз для наибольшего возможного входа. Возможно самое большее p1(n) таких вызовов. Определим длину их входа. Даже если допустить, что алгоритм M1 тратит все его время p1(n) на выписывание входов для M2 , то эти входы не могут быть длиннее, чем p1(n). (Здесь предполагается, что алгоритм может обработать только один символ в каждый момент времени (рассуждения идентичны, если допустить одновременную обработку некоторого постоянного числа символов или даже полиномиального относительно длины входа)). Следовательно, существует полиномиальный алгоритм для П1. ¨
Нам потребуется специальный тип полиномиального сведения. Будем говорить, что задача распознавания П1 полиномиально преобразуется в задачу распознавания П2, если по произвольной данной строке x можно за полиномиальное время относительно ½x½построить такую строку y, что x является индивидуальной задачей для П1 с ответом “да” Û y является индивидуальной задачей для П2 с ответом “да”. Полиномиальные преобразования можно рассматривать как полиномиальные сведения всего лишь с одним вызовом подпрограммы для П2 в конце алгоритма для П1. Остальная часть алгоритма просто строит y - вход соответствующего алгоритма для П2. Говорят, что задача распознавания П Î NP является NP-полной, если все остальные задачи из NP - полиномиально преобразуются в П. Согласно теореме 2, если задача П является NP-полной, то она обладает сильным свойством: если существует эффективный алгоритм для П, то существует эффективный алгоритм для каждой задачи из NP. Класс NP-полных задач обозначим NPC. Понятие NP-полных задач и выдвинутое предположение, что Р ¹ NP приводит к схеме:
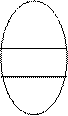 |
NPC
P
Структура класса NP.
Задача П называется NP-трудной, если из существования полиномиального алгоритма для П следует полиномиальный алгоритм для некоторой NP-полной задачи. Чтобы доказать, что некоторая задача NP-полна, необходимо показать, что
а) задача входит в NP,
б) все задачи из NP полиномиально преобразуются в эту задачу. Для доказательства б) достаточно показать, что некоторую известную NP-полную задачу можно полиномиально преобразовать в рассматриваемую задачу. Свойство полиномиальной преобразуемости транзитивно, т.е. если П1 полиномиально преобразуется в П2, П2 полиномиально преобразуется в П3, то П1 полиномиально преобразуется в П3. Однако нужно иметь явное доказательство NP-полноты для первой задачи. Такое доказательство было найдено С.Куком (1971), им была доказана
Теорема 3.3. Задача ВЫПОЛНИМОСТЬ NP-полна.
Доказательство. Пусть ВЫП - идентификатор данной задачи. В предыдущем разделе было показано, что ВЫП ÎNP. Пусть П - произвольная задача из NP. Необходимо показать, что П µ ВЫП. Для этого множество индивидуальных задач 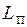 с ответом ДА представим в стандартном виде соответствующей недетерминированной машиной Тьюринга, работающей полиномиальное время и принимающей множество
с ответом ДА представим в стандартном виде соответствующей недетерминированной машиной Тьюринга, работающей полиномиальное время и принимающей множество 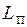 . Такое представление дает общую сводимость задачи, решаемой НДМТ за полиномиальное время.
. Такое представление дает общую сводимость задачи, решаемой НДМТ за полиномиальное время.
Пусть распознающая множество 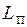 НДМТ имеет алфавиты А,Q и функцию переходов (программу)
НДМТ имеет алфавиты А,Q и функцию переходов (программу)
 ,
,
p(n) - верхняя граница времени вычисления. Функцию 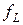 , осуществляющую полиномиальное сведение П µ ВЫП опишем в терминах работы НДМТ.
, осуществляющую полиномиальное сведение П µ ВЫП опишем в терминах работы НДМТ.
В вычислениях участвуют ячейки ленты с номерами от - p(n) до p(n)+1 и при этом требуется учесть не более p(n)+1 тактов работы НДМТ. Проверяющее вычисление определяется заданием в каждый момент времени содержания ячеек с указанными номерами, внутреннего состояния машины и положения считывающей головки. Соответствующие вычисления опишем в виде КНФ, использующей полиномиальное число дизъюнкций. Фиксируем нумерацию в алфавитах:
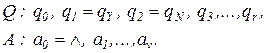
Условимся, что фраза “в момент времени i” означает “после выполнения i-го шага работы”. Если вычисление закончилось раньше времени p(n), то конфигурация не меняется во все моменты после остановки. В нулевой момент на ленте записано слово x в ячейках с номерами 1,...,n. Слово-догадка w пишется в ячейках с номерами ¾1,¾2,...,-|w|. Остальные ячейки пусты. Описывая принимающее вычисление необходимо учесть
а) в ячейках пишется точно один символ;
б) машина находится точно в одном состоянии;
в) головка может просматривать точно одну ячейку с номером от - p(n) до p(n)+1;
г) машина работает по программе.
Определим сначала переменные и их смысл с помощью таблицы:
| Переменная | Пределы изменения индексов | Смысл |
| Q(i,k) | 0 £ i £ p(n), 0 £ k £ r | в момент времени i машина находится в состоянии 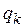
|
| H(i,j) | 0 £ i £ p(n), - p(n) £ j £ p(n)+1 | в момент времени i головка просматривает ячейку с номером j |
| a(i,j,k) | 0 £ i £ p(n), - p(n) £ j £ p(n)+1, 0 £ k £ v | в момент времени i в j-ой ячейке записан символ 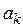
|
Описание сводящей функции 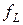 для П µ ВЫП дадим в виде набора дизъюнкций, конъюнкцией которых и будет
для П µ ВЫП дадим в виде набора дизъюнкций, конъюнкцией которых и будет 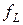 . При этом выполняющий набор значений истинности однозначно соответствует принимающему вычислению на x, стадия проверки занимает время £p(n) шагов, слово-догадка имеет длину £ p(n), причем
. При этом выполняющий набор значений истинности однозначно соответствует принимающему вычислению на x, стадия проверки занимает время £p(n) шагов, слово-догадка имеет длину £ p(n), причем
xÎ 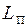 Û на x существует принимающее вычисление
Û на x существует принимающее вычисление
Û на x существует принимающее вычисление с временем £ p(n) и |w|£ p(n)
Û существует выполняющее значение переменных для задачи 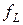 (x), заданной КНФ,
(x), заданной КНФ,
при этом 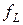 (x) вычисляется за полиномиальное время.
(x) вычисляется за полиномиальное время.
Определим множества дизъюнкций и их смысл.
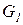 В любой момент времени i машина находится точно в одном состоянии.
В любой момент времени i машина находится точно в одном состоянии.
 В любой момент времени i головка просматривает точно одну ячейку.
В любой момент времени i головка просматривает точно одну ячейку.
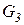 В любой момент времени i каждая ячейка содержит точно один символ A.
В любой момент времени i каждая ячейка содержит точно один символ A.
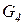 В момент времени 0 вычисление находится в начальной конфигурации стадии проверки со входом x.
В момент времени 0 вычисление находится в начальной конфигурации стадии проверки со входом x.
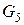 Не более чем через p(n) шагов машина переходит в состояние
Не более чем через p(n) шагов машина переходит в состояние 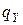 (принимает x).
(принимает x).
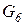 Для любого времени i, 0 £ i £ p(n) конфигурация машины в момент i+1 получается из конфигурации в момент i однократным применением команды машины.
Для любого времени i, 0 £ i £ p(n) конфигурация машины в момент i+1 получается из конфигурации в момент i однократным применением команды машины.
Описание дизъюнкций для функции 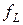 .
.
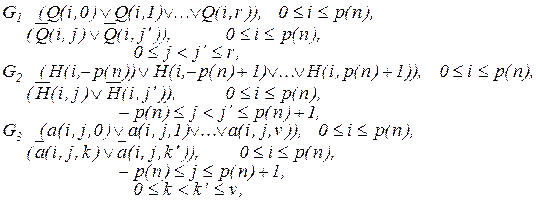

Замечание. Дизъюнкция гарантирует, что если головка машины в момент i не просматривает ячейку j, то в момент i+1 ее содержимое не меняется.
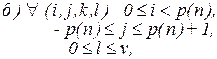
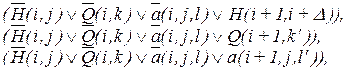
где D,k',l' определены командами машины:
Если 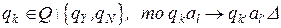 .
.
Если 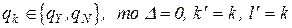 .
.
Заметим, что число дизъюнкций в 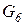 - полином от n. Далее, если xÎ
- полином от n. Далее, если xÎ 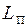 , то существует принимающее вычисление длины £ p(n) и выполнимы все дизъюнкции из
, то существует принимающее вычисление длины £ p(n) и выполнимы все дизъюнкции из  и xÎ
и xÎ 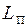 Û существует выполняющий набор для
Û существует выполняющий набор для  . Теперь, для любого xÎ
. Теперь, для любого xÎ 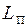 индивидуальная задача
индивидуальная задача 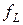 (x) может быть построена за время, ограниченное полиномом от n=|x|, при этом длина
(x) может быть построена за время, ограниченное полиномом от n=|x|, при этом длина 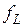 (x) также ограничена сверху полиномом от n.
(x) также ограничена сверху полиномом от n.
Таким образом, преобразование 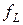 (x) может быть осуществлено за число действий, полиномиально зависящее от n. При этом
(x) может быть осуществлено за число действий, полиномиально зависящее от n. При этом 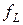 (x) имеет
(x) имеет 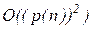 переменных и
переменных и 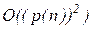 - дизъюнкций. Так как П - произвольная задача из NP, то тем самым теорема доказана.
- дизъюнкций. Так как П - произвольная задача из NP, то тем самым теорема доказана.
3. Другие труднорешаемые задачи. Мы установим NP-полноту еще ряда задач. Для этого покажем, что в рассматриваемую задачу преобразуется задача ВЫПОЛНИМОСТЬ или другая NP-полная задача.
Теорема 3.4. Задача КЛИКА NP-полна.
¨ Уже установлено, что КЛИКАÎNP. Рассмотрим произвольную КНФ f(x1,...,xn). Пусть k - число входящих в нее сомножителей - дизъюнкций. Построим по f граф G следующим образом. Каждому вхождению переменной в формулу сопоставим вершину графа и присвоим ей обозначение (xs,i), где s = 0,1 - данное вхождение, а i - соответствующий номер дизъюнкции. Вершины (xs,i) и (ys,j), соединены ребром тогда и только тогда, когда i ¹ j и xs не является отрицанием yt (т.е. x ¹ y или s=t).
Предположим, что КНФ f(x1,...,xn) выполнима и пусть a - выполняющий ее набор. В каждой дизъюнкции найдется хотя бы одно вхождение, принимающее значение 1. Произвольно выберем по одному такому вхождению и рассмотрим соответствующее множество вершин графа G, данное число вершин равно k - по числу дизъюнкций. Покажем, что любые две из этих вершин соединены ребром. Действительно, ребро между вершинами (xs,i), (ys,j) отсутствует лишь в случае i = j либо yt = 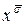 . Но i ¹ y, поскольку вхождения берутся из разных скобок, а yt ¹
. Но i ¹ y, поскольку вхождения берутся из разных скобок, а yt ¹ 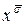 , т.е. одно и то же значение переменной не может одновременно обратить в 1 вхождения xs и
, т.е. одно и то же значение переменной не может одновременно обратить в 1 вхождения xs и 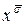 . Значит из выполнимости f следует наличие в G клики размера k.
. Значит из выполнимости f следует наличие в G клики размера k.
Обратно, пусть G содержит клику размера k - ( 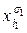 ,j1),..., (
,j1),..., ( 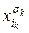 ,jk). Положим (
,jk). Положим ( 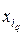 =sq, q =
=sq, q = 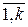 , при этом имеем
, при этом имеем 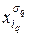 = 1. Значения остальных переменных (если они есть) определим произвольно. Противоречия в этом случае не возникает, ибо если xs и xt соединены ребром, то s=t. По построению графа G вершинам (
= 1. Значения остальных переменных (если они есть) определим произвольно. Противоречия в этом случае не возникает, ибо если xs и xt соединены ребром, то s=t. По построению графа G вершинам ( 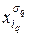 ,jq) соответствуют вхождения из разных сомножителей. Из того, что число вершин равно k, имеем, что каждая дизъюнкция имеет вхождение, обращающее его в 1. При этом КНФ f обращается в 1. ¨
,jq) соответствуют вхождения из разных сомножителей. Из того, что число вершин равно k, имеем, что каждая дизъюнкция имеет вхождение, обращающее его в 1. При этом КНФ f обращается в 1. ¨
Приведем пример.
Пусть дана КНФ f(x1,x2,x3) = (x1Ú 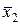 Úx3)(
Úx3)( 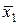 Ú
Ú 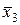 )(x2Ú
)(x2Ú 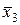 ). Соответствующий граф G имеет вершины:
). Соответствующий граф G имеет вершины:
(x1, 1), ( 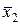 , 1), (x3, 1), (
, 1), (x3, 1), ( 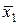 , 2), (
, 2), ( 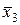 , 2), (x2, 3), (
, 2), (x2, 3), ( 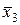 , 3).
, 3).
Соответствующий граф:
( 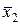 , 1)
, 1)
 |
 (x1, 1) (x3, 1)
(x1, 1) (x3, 1)


 (
( 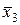 , 3) (
, 3) ( 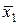 , 2)
, 2)
(x2, 3) ( 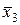 , 2)
, 2)
Клике (x1, 1), ( 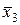 , 3), (
, 3), ( 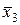 , 2) соответствует набор (1, a, 0), у которого x2- произвольно.
, 2) соответствует набор (1, a, 0), у которого x2- произвольно.
Рассмотрим следующие задачи теории графов:
1. ВЕРШИННОЕ ПОКРЫТИЕ. Для данных графа G(V, E) и целого числа k выяснить, существует ли такое множество вершин C ÍV мощности k , что любое ребро из G инцидентно по крайней мере одной вершине из С.
2. НЕЗАВИСИМОЕ МНОЖЕСТВО. Для данных графа G(V, E) и целого числа k выяснить, существует ли такое множество вершин IÍV мощности k, что никакие две вершины из I не связаны ребром.
Теорема 3.5. Задачи ВЕРШИННОЕ ПОКРЫТИЕ и НЕЗАВИСИМОЕ МНОЖЕСТВО являются NP-полными.
¨ Доказательство осуществляется полиномиальным преобразованием данных задач в задачу КЛИКА. ¨
Рассмотрим теперь следующие задачи булевых функций:
1. РАВНОВЕРОЯТНОСТЬ БУЛЕВОЙ ФУНКЦИИ. Для данной булевойй функции f(x1,...,xn), заданной в КНФ, выяснить, является ли она равновероятностной (т.е. верно ли, что  = 2n-1) ?
= 2n-1) ?
2. ЛИНЕЙНОСТЬ БУЛЕВОЙ ФУНКЦИИ. Для данной булевой функции f(x1,...,xn), заданной в КНФ, выяснить, является ли она линейной?
3. СУЩЕСТВЕННОСТЬ ПЕРЕМЕННОГО. Для данной булевой функции f(x1,...,xn) в КНФ и целого числа k выяснить, является ли переменное xk существенным для f(x1,...,xn) ?
4. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА. Для данной булевой функции f(x1,...,xn) в КНФ выяснить, образует ли f функционально полную систему (является ли шефферовой) ?
Теорема 3.6. Задачи 1 - 4 являются NP-трудными.
¨ 1. Пусть f(x1,...,xn) - произвольная индивидуальная задача ВЫП, причем f(x1,...,xn) º D1×...×Dm, где Di - дизъюнкции. Определим функцию f*(x1,...,xn) º D1...Dm Ú y, где y - новое переменное. Имеем f*(x1,...,xn,y) º D1...DmÚy º (D1Úy)...(DmÚy), откуда следует, что КНФ функции f* строится по функции f за полиномиальное время. Легко видеть, что
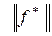 =
= 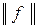 +2n,
+2n,
где 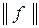 - вес функции f. Отсюда следует, что функция f* равновероятна тогда и только тогда, когда функция f не выполнима. Предположим, что существует полиномиальный алгоритм проверки равновероятности произвольной булевой функции в КНФ. Тогда, применяя его к функции f*, получаем полиномиальный алгоритм проверки выполнимости КНФ функции f.
- вес функции f. Отсюда следует, что функция f* равновероятна тогда и только тогда, когда функция f не выполнима. Предположим, что существует полиномиальный алгоритм проверки равновероятности произвольной булевой функции в КНФ. Тогда, применяя его к функции f*, получаем полиномиальный алгоритм проверки выполнимости КНФ функции f.
2. Пусть f(x1,...,xn) - произвольная индивидуальная задача ВЫП. Рассмотрим функцию f*(x1,...,xn,y1,y2) º f(x1,...,xn)×y1 Ú y2, где y1, y2 - новые переменные. Ясно, что КНФ функции f* строится по функции f за полиномиальное время. Легко видеть, что функция f* является линейной тогда и только тогда, когда функция f не выполнима. Значит, если существует полиномиальный алгоритм распознавания линейности, то, применяя его к функции f*, получаем полиномиальный алгоритм проверки выполнимости произвольной КНФ.
3. Пусть f(x1,...,xn) - произвольная индивидуальная задача ВЫП. Положим f*(x1,...,xn,y) º f(x1,...,xn)×y , где y - новое переменное. Функция f* в КНФ строится по функции f за полиномиальное время. Легко видеть, что переменное y существенно для функции f* тогда и только тогда, когда f выполнима. Значит, если существует полиномиальный алгоритм проверки существенности любого переменного, то, применяя его к функции f*, при y º xk получаем полиномиальный алгоритм проверки выполнимости произвольной КНФ.
4. Пусть f(x1,...,xn) - произвольная индивидуальная задача ВЫП. Рассмотрим функцию
f*(x1,...,xn,y1,y2,y3) º f(x1,...,xn,) 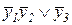 ,
,
где y1, y2, y3 - новые переменные. Ясно, что КНФ функции f* строится по функции f за полиномиальное время. Функция f* образует функционально полную систему тогда и только тогда, когда функция f выполнима.
Действительно, если f не выполнима, то f* º 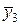 и значит, f* не является функционально полной. Если f выполнима, то пусть x1,...,xn - выполняющий ее набор. Тогда имеем
и значит, f* не является функционально полной. Если f выполнима, то пусть x1,...,xn - выполняющий ее набор. Тогда имеем
f*(x1,...,xn,0,0,1) º f*( 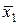 ,...,
,...,  ,1,1,0) º 1,
,1,1,0) º 1,
f*(x1,...,xn,0,0,0) º f*(x1,...,xn,0,0,1) º 1.
Отсюда следует не самодвойственность и не линейность функции f*. Легко видеть, что f* не сохраняет ноль, не сохраняет единицу и не монотонна. Значит, функция f* удовлетворяет критерию функциональной полноты. Если существует полиномиальный алгоритм проверки функциональной полноты булевой функции, то, применяя его к функции f*, получаем полиномиальный алгоритм проверки выполнимости произвольной КНФ. ¨
Замечание. Нетрудно убедиться, что задачи “НЕЛИНЕЙНОСТЬ БУЛЕВОЙ ФУНКЦИИ” (отрицание задачи 2), “СУЩЕСТВЕННОСТЬ ПЕРЕМЕННОГО” лежат в классе NP и в силу доказанного они NP-полны. Неизвестно, верно ли это для задачи 1 и 4. При изменении способа задания булевой функции может измениться класс сложности задачи. Так, при табличном задании булевой функции рассмотренные задачи имеют полиномиальную сложность.
Определим задачу k-ВЫПОЛНИМОСТИ ( k- некоторое фиксированное натуральное число). Задача k-ВЫПОЛНИМОСТИ (сокращенно: k-ВЫП) отличается от задачи ВЫП только тем, что в задаче k-ВЫП в каждой дизъюнкции Di (см. определение задачи ВЫП) не более k литералов. Ясно, что задача 1-ВЫП является полиномиальной. Далее (лемма 1.1 главы 3) будет показано, что задача 2-ВЫП полиномиальна.
Теорема 3.7.Задача 3-ВЫП является NP-полной.
¨ Пусть
f º 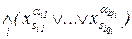
- некоторая индивидуальная задача из задачи ВЫП. Этой формуле сопоставим формулу f¢ из задачи 3-ВЫП, при этом для каждой дизъюнкции  , содержащей qi литералов, введем qi-3 новых переменных yi1,yi2,...,
, содержащей qi литералов, введем qi-3 новых переменных yi1,yi2,..., 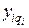 , каждую дизъюнкцию формулы f заменим на k-2 дизъюнкций в формуле f¢ по правилу: если f имела дизъюнкцию
, каждую дизъюнкцию формулы f заменим на k-2 дизъюнкций в формуле f¢ по правилу: если f имела дизъюнкцию  , то заменяем ее на конъюнкцию дизъюнкций
, то заменяем ее на конъюнкцию дизъюнкций
(x1Úx2Úy1)(x3Ú 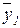 Úy2)(x4Ú
Úy2)(x4Ú 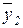 Úy3)...(xk-2Ú
Úy3)...(xk-2Ú  Úyk-3)(xk-1ÚxkÚ
Úyk-3)(xk-1ÚxkÚ 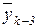 ).
).
Формулы f и f¢ одновременно выполнимы или невыполнимы (доказательство этого факта оставляем читателю). ¨
В настоящее время установлена труднорешаемость большого числа (несколько тысяч) задач из различных областей дискретной математики. Мы ограничились рассмотрением только отдельных их представителей, связанных с основной тематикой курса. Для более полного ознакомления с состоянием дел в данной проблематике следует обратиться к соответствующей журнальной литературе. Заметим, что установление труднорешаемости конкретной задачи дает важную в практическом отношении информацию. В этом случае целесообразно сосредоточиться на поиске удовлетворительных алгоритмов экспоненциальной сложности либо разрабатывать эффективные (полиномиальные) алгоритмы для частных случаев исходной задачи.
Проверочные вопросы и упражнения к § 3
1. Сформулируйте задачу ВЫПОЛНИМОСТЬ.
2. Покажите, что задача КЛИКА полиномиальна, если k - некоторая константа (например, k = 3).
3. Пусть задача П принадлежит классу NP. С какой сложностью эта задача может быть решена на детерминированной машине Тьюринга.
4. Приведите пример двух задач, одна из которых полиномиально сводится к другой.
5. В каком случае NP-полная задача может быть полиномиально сведена к полиномиальной задаче.
6. Какая задача явилась первой NP-полной задачей?
7. Докажите, что задача СУЩЕСТВЕННОСТЬ ПЕРЕМЕННОЙ является NP-полной.
8. Докажите, что формулы f и f¢ из доказательства теоремы 3.7 одновременно выполнимы или невыполнимы.
9. Докажите, что при любом k³4 задача k-ВЫП является NP-полной.
Дата добавления: 2014-12-02; просмотров: 1873;
