Проблема самоприменимости.

Данная проблема заключается в следующем. Будем рассматривать машины Тьюринга, которые во внешнем алфавите ленты имеют 0, 1. Пусть на ленту машины Тьюринга Т записан ее код Код(Т) и машина запущена в начальном состоянии q₁ . Если после конечного числа шагов машина Т остановится, то она называется самоприменимой, в противном случае - несамоприменимой. Легко привести примеры самоприменимых и несамоприменимых машин. Проблема самоприменимости состоит в том, чтобы по всякой машине Тьюринга Т (точнее по ее коду Код(Т)) установить, является ли она самоприменимой или нет. Будем говорить, что машина Тьюринга Т₀ решит проблему самоприменимости, если для любой машины Т конфигурацию q₁Код(Т) она переводит в конфигурацию q₀1, если Т самоприменима, и в конфигурацию q₀0, если Т - несамоприменима.

Теорема 1.1. Не существует машины Тьюринга Т₀ , которая решает проблему самоприменимости.

¨ Допустим, что существует машина T₀, решающая проблему самоприменимости. Построим машину T₁, в которой вместо состояния q₀ введем новое заключительное состояние q₀¢ и добавим к программе машины T₀ новые команды

q₀ 1 ® q₀ 1 E,

q₀ 0 ® 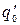0 E. (1.4)

Машина T₁ построена по машине T₀ вполне конструктивными средствами, она обладает свойствами применимости к кодам несамоприменимых машин и не применима к кодам самоприменимых машин. Действительно, если Т₁ - самоприменима, то q₁Код(Т₁) переходит в q₀1 и согласно (1.4) q₀1 Þ q₀1 и T₁ никогда не остановится. Если T₁ - несамоприменима, то q₁Код(Т) переходит в q₀0 и согласно (1.4) q₀0 Þ q₀¢0 и машина Т₁ остановится. Применим теперь машину T₁ к конфигурации q₁Код(Т₁). Если T₁ самоприменима, то по построению она не применима к коду самоприменимых машин. Если T₁ несамоприменима, то она применима к коду самоприменимых машин. Полученное противоречие показывает, что допущение о существовании машины Тьюринга T₀, решающей проблему самоприменимости, неверно. ¨

В силу тезиса Тьюринга невозможность построения машины Тьюринга означает отсутствие алгоритма решения данной проблемы. Поэтому данная теорема дает первый пример алгоритмически неразрешимой проблемы.

Отсюда вытекает еще пример алгоритмически неразрешимой проблемы - проблемы останова. Она состоит в том, чтобы по машине Т и начальной конфигурации q₁a узнать, остановится ли Т через конечное число шагов.

Проблема останова алгоритмически неразрешима. Если бы она была алгоритмически разрешимой, то взяв в качестве a код машины Т, можно было бы решить проблему самоприменимости. Данные теоремы лежат в основе доказательства алгоритмической неразрешимости большого числа алгоритмических проблем. При истолковании утверждений, связанных с алгоритмической неразрешимостью, следует иметь в виду следующее обстоятельство. Речь идет об отсутствии единого алгоритма, решающего данную проблему, при этом не исключается возможность ее решения в частных случаях.

Неразрешимость проблемы останова можно интерпретировать как несуществование общего алгоритма для отладки программ, точнее, алгоритма, который по тексту любой программы и данным для нее определял бы, зациклится ли программа на этих данных или нет.

Приведем без доказательства важную теорему теории алгоритмов.

Теорема 1.2(теорема Райса). Никакое нетривиальное свойство вычислимых по Тьюрингу функций не является алгоритмически разрешимым.

Переформулируем эту теорему в более точном виде: Пусть С - любой класс вычислимых по Тьюрингу функций одного переменного, нетривиальной в том смысле, что имеются вычислимые функции, как входящие в С, так и не входящие в С. Тогда не существует алгоритма, который бы по номеру x функции f_x определял бы принадлежность f_x классу С.

Из данной теоремы следует, что по номеру вычислимой функции нельзя узнать, является ли она постоянной, периодической, ограниченной и т.п. Смысл данной теоремы в том, что по описанию алгоритма нельзя узнать о свойствах функций, которую он вычисляет. Подчеркнем, что “нельзя узнать” означает “не существует единого алгоритма решения”. Свойства подклассов вычислимых функций могут оказаться разрешимыми.