Машина Тьюринга.

Машина Тьюринга (детерминированная машина Тьюринга) состоит из следующих элементов:

1) Ленты, разбитой на ячейки, в каждой из которых может быть записан один из символов конечного алфавита А = {a₀,a₁,…,a_m}.

2) Управляющего устройства, которое может находиться в одном из конечного числа состояний, образующих множество Q = {q₀,q₁,…,q_n}.

3) Считывающей/пишущей головки, которая в каждый момент времени обозревает ячейку ленты и в зависимости от символа в этой ячейке и внутреннего состояния записывает в эту ячейку символ, сдвигает считывающую головку на один шаг вправо, или влево, или остается на месте, при этом машина переходит в новое внутреннее состояние. Таким образом, действие машины Тьюринга определяется системой команд вида

q_i a_j ® q_k a_l d, (1.1)

где a_j - считываемый символ, q_i - внутреннее состояние, q_k - новое внутреннее состояние, a_l - новый записываемый символ, d - направление движения головки, обозначаемое одним из символов L (влево), R (вправо), E (на месте).

Среди состояний машины выделены начальное состояние - q₁ и заключительное состояние - q₀. Перед началом работы машина устанавливается в начальное состояние, попав в заключительное состояние, машина останавливается.

Лента является бесконечной в обе стороны, однако в начальный момент времени только конечное число ячеек заполнено непустыми символами, остальные ячейки пусты, т.е. в них записан выделенный символ a₀. Следовательно, и в любой другой момент времени лишь конечное число ячеек будет содержать непустые символы. Таким образом, для машины Тьюринга данные - это слова в алфавите ленты А = {a₀,a₁,…a_m}. Память является внутренней - это состояния машины Q = {q₀,q₁,…,q_n} и внешней - это лента машины. Детерминированность обеспечивается системой команд вида (1.1) для каждого a_j Î А, и каждого q_i Î Q\q₀ , т.к. символ q₀ не может встречаться в левых частях команд. Совокупность внутреннего состояния, состояния ленты (т.е. слова, записанного на ленте), положения головки на ленте называется конфигурацией или машинным словом и обозначается

a₁ q_i a₂ , (1.2)

где q_i - внутреннее состояние, a₁ - слово, состоящее из непустых символов алфавита А, стоящее слева от головки, a₂ - слово из считываемого символа и непустых символов справа от головки. Стандартная начальная конфигурация имеет вид q₁a , стандартная конечная конфигурация имеет вид q₀a. Приведем блок-схему машины Тьюринга:

q_i

Если К - незаключительная конфигурация, то однозначно определена следующая конфигурация К¢. Это обстоятельство запишем в виде К ® К¢. Если для конфигураций К₁ и К_t выполнено К₁ ® К₂ ® … ® К_t , то это будем обозначать в виде К₁ Þ К_t . Определим теперь вычисление с помощью машин Тьюринга. Исходными данными машины Тьюринга являются слова в алфавите исходных данных А_исх (А_исх Í А) или наборы таких слов. Набор слов назовем правильным, если он имеет вид a₁*a₂*…*a_k, где * - символ-разделитель, не входящий в А_исх. Пусть А_рез (А_рез Í А) - алфавит результатов. Пусть f(a₁,…,a_k) - функция над наборами длины k слов в алфавите А_исх со значением в множестве слов в алфавите А_рез. 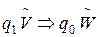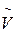Машина Т правильно вычисляет функцию f, если для любых V и W, таких, что f(V) = W, справедливо , где и 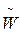- правильные записи V и W соответственно, причем для любого V, такого, что f(V) не определена, машина Т, запущенная в стандартной начальной конфигурации работает бесконечно. Если для функции f существует машина Тьюринга Т, которая ее правильно вычисляет, то функция f называется правильновычислимой по Тьюрингу. С другой стороны, всякой правильно вычисляющей машине Тьюринга Т можно поставить в соответствие вычисляемую функцию f_T

Пример. Пусть А = {a₀, a₁}, Q = {q₀, q₁}.

Список команд : q₁ a₀ ® q₀ a₁ E, (1.3)

Т q₁ a₁ ® q₁ a₁ R.

Будем кодировать натуральные числа n в виде n+1 подряд идущих символов 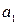(Обозначение - n: = ). Тогда легко видеть, что всякая начальная конфигурация вида 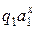переходит в заключительную вида 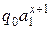. Таким образом, машина Тьюринга (1.3) вычисляет функцию

f(x) = x + 1.

Тезис Тьюринга. Для всех процедур, претендующих на алгоритмичность, удается построить реализующие их машины Тьюринга. В связи с этим А.Тьюринг выдвинул следующий тезис: “Всякий алгоритм может быть реализован на машине Тьюринга”. Доказать данный тезис нельзя, поскольку понятие алгоритма является неточным. Подтверждением данному тезису является математическая практика, а также то обстоятельство, что описание алгоритма в любой другой известной алгоритмической модели сводится к описанию его в виде машины Тьюринга. Однако, принятие тезиса Тьюринга позволяет истолковывать утверждения о несуществовании машин Тьюринга для решения конкретных задач как утверждения о несуществовании алгоритмов вообще.