Лекция 2. Машина Тьюринга

Включают в себя следующие управленческие действия:

§ разъяснение требований к работе;

§ использование координационных и интеграционных механизмов ( иерархии полномочий, цепи команд, единоначалия, работы координационных отделов, совещаний);

§ установление общеорганизационных комплексных целей, формирование корпоративного духа;

§ использование системы вознаграждения людей, вносящих свой вклад в достижение общеорганизационных целей.

Лекция 2. Машина Тьюринга

В 1936 году независимо одна от другой появились работы английского математика А. Тьюринга и американского математика Э. Поста, в которых были даны уточнения понятия алгоритма или "эффективной процедуры" для решения массовых задач в терминах некоторых идеализированных вычислительных машин, называемых теперь машинами Тьюринга или Тьюринга-Поста. Устройства этих машин у А. Тьюринга и Э. Поста отличаются лишь несущественными деталями, а именно, процедура вычислений у Э. Поста раздроблена на более мелкие операции, чем у А. Тьюринга. В настоящее время в литературе описано много различных модификаций таких идеализированных машин. Мы далее рассмотрим одну из них, называя ее машиной Тьюринга (сокращенно МТ).

Машина Тьюринга, как и нормальный алгоритм, предназначается для переработки слов в некотором конечном алфавите 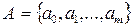, называемом внешним алфавитом машины. Слова в алфавите А записываются на ленту МТ, разбитую на ячейки, так, что в каждую ячейку записывается какая-либо одна буква алфавита А. Сама лента называется внешней памятью МТ. Предполагается, что лента в процессе работы может наращиваться, т.е. ленту можно считать потенциально бесконечной в обе стороны. Все вновь пристраиваемые ячейки заполняются символом 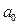, который называется пустым символом.

Переработка слов, записываемых на ленту МТ, осуществляется в дискретном времени по тактам, занумерованным натуральными числами, под действием так называемого управляющего устройства. Последнее в каждый такт может находиться в одном из конечного множества состояний

,

называемых внутренним состоянием.

Управляющее устройство связано с лентой так называемой считывающей головкой, которая в каждый такт находится против одной из ячеек ленты (обозревает одну ячейку). По команде управляющего блока, зависящей от внутреннего состояния и от содержимого обозреваемой ячейки, машина или останавливается или переходит в новое состояние, в последнем случае головка заменяет символ обозреваемой ячейки новым символом из Аи остаётся против той же ячейки, или сдвигается на одну ячейку влево. При этом если головка обозревала последнюю (правую) ячейку ленты и ей дана команда сдвинуться вправо (влево), то к ленте справа (слева) автоматически добавляется новая ячейка с буквой . Оказавшись в состоянии , МТ прекращает работу ( называют стоп-состоянием).

Из приведённого описания видно, что положение МТ в каждый момент времени полностью определяется следующими параметрами:

1. словом, записанным на ленте;
2. внутренним состоянием;
3. номером обозреваемой ячейки.

Если в некотором такте работы МТ на её ленте записано слово , управляющее устройство находится в состоянии и головка обозревает ячейку с номером , то всю эту информацию можно записать одним, так называемым машинным, словом

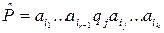
(символ внутреннего состояния записывается перед буквой, записанной в обозреваемой ячейке). При переходе к новому такту машинное слово меняется согласно системе команд МТ. Изменения зависят от состояния МТ и от содержимого обозреваемой ячейки. Поэтому каждая команда записывается в виде формулы

, (1)

где 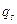- новое состояние, - буква, на которую заменяется 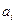(не исключается случай ), - одна из букв H, R, L, которые означают соответственно сохранение положения головки, сдвиг её на одну ячейку вправо, сдвиг на одну ячейку влево. Слова 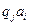, 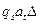называются соответственно левой и правой частями команды.

Подчеркнём, что система команд МТ удовлетворяет следующему единственному условию детерминизма: каждое слово вида 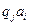(если не стоп-состояние) является левой частью ровно одной команды. Это условие позволяет всю систему команд МТ записать в виде таблицы.

Таблица 1.

Q A			…		…
	…	…	…	…	…	…
. …
	…	…	…		…	…
……
	…	…	…	…	…	…

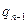
Заметим, что в левых частях команд, а потому и во входной строке таблицы, состояние не участвует, поскольку в состоянии МТ прекращает работу.

Опишем теперь процесс преобразования слов в алфавите Aописанной выше МТ с системой команд S.

В начале работы с МТ устанавливается в состояние , на её ленту записывается исходное слово и считывающая головка помещается против 1-й (самой левой) ячейки (т.е. обозревает 1-ю букву слова ).

Если , то вся информация о начале работы запишется машинным словом

.

Теперь, как и при описании работы НА, сопоставим слову конечную или бесконечную последовательность машинных слов

(2)

Для этого находим в Sкоманду вида

и в зависимости от значения , равного H, R или L, в качестве берём соответственно слово

Если 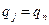, то в качестве искомой возьмём двухэлементную последовательность 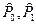. В противном случае, как и выше, построим слово 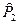и т.д. Продолжая этот процесс, мы и получим искомую последовательность (2).

Последовательность слов в алфавите A, полученных удалением из слов символов-состояний, назовём путём переработки слова .

Если последовательность (2) конечна и оканчивается словом 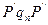то говорят, что машина применима к слову и перерабатывает его в слово . Этот факт записывают в виде

.

Если же последовательность (2) бесконечна, то говорят, что машина не применима к слову .

Таким образом, любая МТ осуществляет частичное отображение множества слов в алфавите Aв себя.

Приведем пример МТ, осуществляющей удвоение натуральных чисел. Как и при построении НА, натуральное число 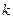будем изображать в виде последовательности 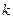вертикальных чёрточек. В качестве внешнего алфавита возьмем множество , где 0 – пустой символ, а в качестве внутреннего –

.

Систему команд зададим таблицей:

Таблица 2.

Q A
|

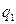
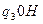
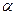
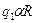
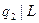
В начале работы на ленту записывается слово 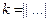, а вся информация о начале работы определится машинным словом

.

В качестве упражнения постройте последовательность машинных слов, начинающуюся словом .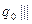

Из сравнения определений НА и МТ видно, что в последний процесс преобразования слов разбит на более мелкие операции – них в каждый такт заменяется не более одной буквы слова. Кроме того, в них есть и другое сильное ограничение – расширение слова может происходить только за счёт приписывания новых символов слева или справа от слова (т.е. в начале его или конце). В связи с этим строить НА для решения задач, как правило проще, чем МТ. Так, задачу удвоения натурального числа можно решить НА со схемой

,

,

.

В нем всего лишь три команды вместо 9 в построенной выше машине, да и число тактов работы по удвоению слова существенно меньше. На первый взгляд может казаться, что и в принципе МТ имеют меньше возможностей по сравнению с НА. Однако А. Тьюрингом и Э. Постом была выдвинута гипотеза (или тезис) о том, что любой алгоритм над алфавитом A эквивалентен относительно A алгоритму, осуществляемому подходящей машиной Тьюринга (соответственно Поста).

Как и тезис Маркова А. А. Нормализации алгоритмов, эта гипотеза не может быть доказана, её можно лишь подкреплять какими-либо разумными доводами. Наиболее важным из них является известная к настоящему времени теорема о том, что всякий НА осуществим на МТ.