Дифференциальное действие по скорости изменения PV
На практике оператор производит внезапное изменение уставки много раз. Это приводит к внезапному изменению отклонения, ведущему к высокому дифференциальному броску.
Такой внезапный толчок может быть неблагоприятен для стабильной реакции, и его следует избегать. Одним из способов избежать данного толчка является основание дифференциального действия на изменении контролируемой переменной, PV, а не изменении отклонения. Поскольку отклонение определяется как SP - PV, измененное PID уравнение с ослабленной дифференциальной составляющей может быть выражено следующим образом:
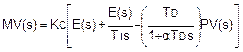
Это выражение называется форма отклонения для PID уравнения. Алгоритм управления, который мы изучали до сих пор, был основан на величине отклонения. Он имеет смысл, поскольку алгоритмы управления предназначены для того, чтобы сводить отклонения к минимуму. Теперь вместо отклонения в данном уравнении для дифференциальной составляющей используется PV. Какой в этом смысл?
Если уставка остается постоянной, то изменение отклонения остается таким же, как изменение контролируемой переменной, PV. Таким образом, действие данного, основанного на PV PID алгоритма является таким же, как у алгоритма на основе отклонения, когда уставка остается неизменной.
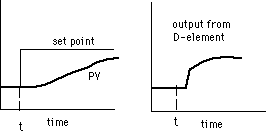
Когда уставка изменена, дифференциальная составляющая в начале не выполняет каких-либо действий, поскольку немедленного изменения PV не происходит. Таким образом, исключается начальный дифференциальный бросок.
Однако, действуют пропорциональная и интегральная составляющие, перемещая PV в сторону уставки, поскольку их расчет выполняется на основе величины отклонения.
Данный метод устранения нежелательного дифференциального броска является стандартным свойством многих промышленных PID-контроллеров.
Очень часто пропорциональный бросок для изменения уставки является нежелательным. Отсюда предусматривается дополнительная форма PID уравнения, в которой пропорциональное изменение основано на скорости изменения PV, а не отклонения. Его называют PV формой для PID уравнения.
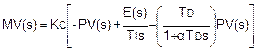
Дата добавления: 2014-12-02; просмотров: 1127;
