Промышленный PID-контроллер

Алгоритм PID управления, который мы до сих пор использовали, называется идеальным алгоритмом PID управления.

В форме дифференциального уравнения он имеет следующее выражение:

В системе Лапласа это выражается следующим образом:

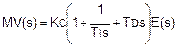
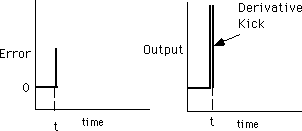
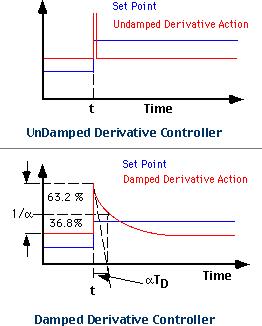
Как мы уже знаем, дифференциальное действие очень чувствительно к внезапному изменению отклонения, что приводит к дифференциальному броску.

Если оператор внезапно производит большое изменение уставки, это приводит к большому изменению отклонения. Пропорциональная составляющая реагирует с относительно невысоким пропорциональным броском, что обычно желательно, поскольку быстро приводит контролируемую переменную на уровень уставки. Однако, сильный дифференциальный бросок, вызванный дифференциальной составляющей, может привести к нестабильному состоянию.

В условиях реальной установки некоторые измеренные переменные процесса имеют значительные помехи, вызванные механическими и электронными устройствами для измерения и передачи. Колебания PV из-за помех вызывают появление искусственных колебаний значений отклонения, что вызывает ненужную реакцию дифференциальной составляющей.

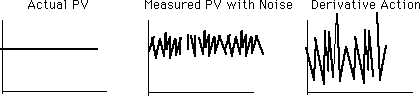
Поэтому рекомендуется избегать дифференциального управляющего действия для таких "шумящих" приборов, как регуляторы расхода. Следует помнить, что дифференциальное действие можно отключить, настроив время дифференцирования на нуль, из-за чего PID-контроллер будет действовать как PI-контроллер.

Ослабление дифференциального действия

Гиперчувствительный характер дифференциального действия можно свести к минимуму, добавив в дифференциальную составляющую запаздывание первого порядка.

Идеальный дифференциальный алгоритм по системе Лапласа имеет следующее выражение:

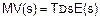
Добавив запаздывание первого порядка, можно выразить этот алгоритм следующим образом:

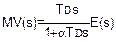
Где:

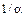— , который называется "дифференциальное усиление". Также он известен как коэффициент усиления или динамический предел усиления. Обычно его значение настраивают на 10.

Коэффициент усиления, равный 10( 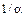), означает, что на одно единичное изменение отклонения дифференциальный выход увеличится на 10( 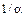), а затем будет угасать в течение некоторого времени. Таким образом, дифференциальный бросок ограничивается в пределах приемлемого диапазона и медленно угасает в сравнении с импульсной реакцией идеальной дифференциальной составляющей.

За время дифференцирования " ", выход контроллера уменьшится на 63,2% от дифференциального броска, как в системе первого порядка. Влияние дифференциального действия длится больше с возрастанием времени дифференцированияили уменьшением коэффициента усиления ( ).

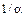Измененное уравнение PID с ослабленной дифференциальной составляющей в системе Лапласа можно выразить следующим образом:

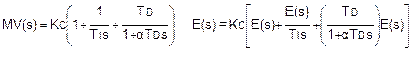
Это измененное дифференциальное уравнение является стандартным свойством многих промышленных PID-контроллеров.