Система первого порядка

На данный момент мы узнали, что протекание процесса в динамических условиях можно описать усилением, постоянной времени и "мертвым" временем.

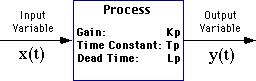
Для того чтобы учитывать динамику процесса при расчете и анализе схемы управления процессом, требуется выразить протекание в динамических условиях с математической точки зрения.

Протекание в динамических условиях большинства процессов без "мертвого" времени можно приблизительно выразить математически при помощи линейного дифференциального уравнения первого порядка,

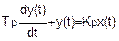
где:

K_p — усиление процесса,

T_p — постоянная времени,

t — время,

y(t) — выходное значение в момент t,

x(t) — входное значение в момент t.

Это простейшее представление процесса в математической форме, которое часто используется для анализа управления технологическим процессом.

Данное дифференциальное уравнение является дифференциальным уравнением первого порядка, так как такое представление процесса называется системой запаздывания первого порядка. Любой процесс, который можно выразить данным уравнением, называется процессом запаздывания первого порядка или просто процессом первого порядка.

Решение данного уравнения позволяет получить динамическую реакцию выходного параметра, y. В случае игнорирования "мертвого" времени решение для единичного скачкообразного изменения на входе будет иметь следующий вид:

Теперь составим проекцию различных значений выходного параметра, y, на различные значения времени, t. Данная кривая очень напоминает динамическую реакцию, которую мы изучили ранее на примерах бака и печи. Выполним дальнейший анализ реакции.

- Максимальная скорость изменения выходного параметра возникает в начале, а затем непрерывно падает.

- Если бы изменение выходного параметра происходило постоянно на максимальной скорости, то параметр достиг бы своего конченого значения за одну постоянную времени.

- С течением времени выходной параметр приближается к значению, равному усилению его процесса.

При t = ∞, уравнение принимает следующий вид ,

- При величине времени t, равной постоянной времени, Tp, уравнение процесса первого порядка имеет следующий вид:

Это подразумевает, что для процесса первого порядка выходной параметр достигает 63,2% своего конченого значения за время, равное одной постоянной времени. Это очень важное значение, т.е. если мы можем измерить время, необходимое, чтобы выходной параметр достиг 63,2% своего конечного значения, то мы можем посчитать постоянную времени данного процесса.

Постоянная времени позволяет получить особый динамический взгляд на быстроту реакции системы, т.е. является мерой скорости реакции.

Во многих учебниках по управлению технологическими процессами вместо дифференциального уравнения применяется уравнение переноса Лапласа. В системе Лапласа уравнение процесса первого порядка может быть выражено следующим образом:

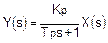
где:

K_p — усиление процесса,

T_p — постоянная времени,

s — оператор Лапласа,

Y(s) — выходное значение в системе Лапласа,

X(s) — входное значение в системе Лапласа

На данный момент мы узнали о приближении первого порядка для процесса без "мертвого" времени. Для процессов с "мертвым" временем приближение первого порядка имеет следующий вид,

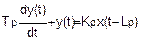
где:

K_p — усиление процесса,

T_p — постоянная времени,

L_p — "мертвое" время,

t — время,

y(t) — выходное значение в момент t,

x(t) — входное значение в момент t.

Данное представление процесса называется системой запаздывания первого порядка с "мертвым" временем. Любой процесс, который можно выразить данным уравнением, называется процессом запаздывания первого порядка с "мертвым" временем или просто процессом первого порядка с "мертвым" временем.

В системе Лапласа процесс запаздывания первого порядка с "мертвым" временем имеет следующее выражение:

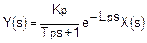
где:

K_p — усиление процесса,

T_p — постоянная времени,

L_p — "мертвое" время,

s — оператор Лапласа,

Y(s) — выходное значение в системе Лапласа,

X(s) — входное значение в системе Лапласа