Решение. f"'(х) = 2 (1+ х)-3, f""(х) = - 2 * 3(1 + х)-4;
F' (х) = 1/ (1 + х) = (1 + х)-1; f"(х) = - (1 + х)-2 ;
f"'(х) = 2 (1+ х)-3, f""(х) = - 2 * 3(1 + х)-4;
f5 (х) = 2 * 3 * 4 (1 + х)-5, .......
подставим х = 0:
f (0) = ln (1+ 0) = 0, f' (0) = (1+ 0)-1 = 1,
f"(0) = -1, f"'(0) = 2, f""(0) = - 2 * 3, f5 (0) = 2 * 3 * 4,..........
Ряд имеет вид ln (1+ х) = 0 + 1 * х - 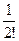 х2 +
х2 + 
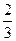 х3 -
х3 - 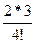 х4 +
х4 + 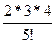 х5 – или ln (1+ х) = х1 – х2/2 + х3/3 – х4/4 + х5/5 - ...........
х5 – или ln (1+ х) = х1 – х2/2 + х3/3 – х4/4 + х5/5 - ...........
Интервал сходимости: -1 < x < 1.
Основные разложения в ряд Маклорена.
Ниже приведены пять основных разложений и указаны интервалы сходимости:
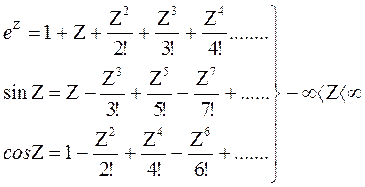
ln (1+ Z) = Z - 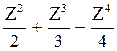 +....... –1 < Z < 1,
+....... –1 < Z < 1,
(1 + Z)m = 1 + m Z + 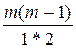 Z2 +
Z2 + 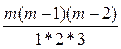 Z3 +
Z3 + 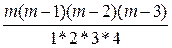 Z4 + ...... , –1 < Z < 1.
Z4 + ...... , –1 < Z < 1.
Последний ряд называется БИНОМИАЛЬНЫМ (m может быть любым числом, в том числе дробным и отрицательным).
Вычисление значений функций с помощью рядов.
Пример. С точностью до 0,001 вычислить ln 1,2.
Решение. ln 1,2 = ln (1 + 0,2). Так как Z = 0,2 находится внутри промежутка –1 < Z < 1, то это значение можно подставить в разложении функции ln (1 + Z):
Ln(1 + 0,2) = 0,2 – 0,22/2 + 0,23/3 – 0,24/4 +.......≈ 0,2 – 0,02 + 0,00267 – 0,0004 + .... ≈ 0,2 – 0,02 + 0,00267 ≈ 0,183
ln 1,2 ≈ 0,183.
ЭВМ вычисляют значения функций с помощью рядов.
Вычисление определенных интегралов с помощью рядов.
Ряд Тэйлора
Ряд Маклорена обычно используют для представления функции в окрестности точки х = 0. Для представления функции в окрестности точки х = х0 ≠ 0, удобнее ряд Тэйлора : f (х) = f (х0) + f'(х0) (х – х0) + 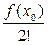 (х – х0)2 +
(х – х0)2 + 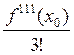 (х-х0)3 +
(х-х0)3 + 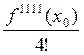 (х-х0)4 + ....
(х-х0)4 + ....
2. ТЕОРИЯ ВЕРОЯТНОСТЕЙ.
2.1. Случайные события
Классическое определение вероятности.
Событие, которое в результате данного испытания может появиться, а может и не появится СЛУЧАЙНЫМ.
Например: испытание – подбрасывание монеты; случайное событие – выпадение герба.
События обозначают буквами А, В, С, ...
Количественной оценкой возможности появления события является его вероятность.
Вероятность события А обозначают Р (А) или р.
В ряде случаев вероятности события можно – подсчитать, используя классическое определение вероятности:
Р = m/п
Здесь п – общие число равновозможных исходов испытания;
m- число тех из них, которые благоприятствуют появлению события.
n-
Пример. В ящике 5 шаров – 3 черных и 2 белых. Наугад вынимают один шар. Найти вероятность того, что он окажется черным.
Решение. Р = 3/5. («Равновозможность исходов испытания в данном случае означает, что шары неразличимы «на ощупь»).
Свойства вероятностей.
Событие называется достоверным, если в результате данного испытания оно обязательно проявляется.
Например, выпадение хотя бы одного очка при подбрасывании игральной кости (кубика).
Для достоверного события m = п 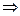 р = 1
р = 1
Вероятность достоверного события равна единицы
Если событие случайно, то 0 < m < n 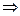 0 < m < n < 1,
0 < m < n < 1,
т.е. для случайного события 0 < р < 1.
Если появление некоторого события в данном испытании невозможно, то m = 0 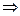 р = 0.
р = 0.
Вероятность невозможного события равна нулю.
Устойчивость относительной частоты.
Повторим испытание много раз и запомним, сколько раз случайно событие появилась.
Отношение числа появлений события к числу испытаний называется его относительной частотой.
Например, при ста подбрасываниях монеты герб выпал 53 раза. Значит, относительная частота выпадений герба равна 53/100 = 0,53.
Наблюдения показывает, что относительная частота обладает свойством устойчивости:
При большом числе испытаний относительная частота события близка к его вероятности (и тем ближе, чем больше испытаний).
Так, в приведенном выше примере относительная частота выпадений герба 0,53 близка к вероятности этого события ½ = 0,5.
Свойство устойчивости позволяет предсказать, сколько примерно раз событие появится при заданном числе испытаний.
Пример. Сколько примерно раз выпадает единица при 1200 подбрасываниях игральной кости?
Решение. Вероятность выпадения единицы равна 1/6
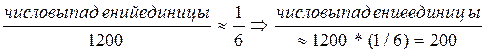 ≈
≈
Статистическое определение вероятности.
Для многих событий невозможно подсчитать вероятность классическим способом. Например, вероятность попадания в цель при выстреле. Однако наблюдения показывают, что и для таких событий относительная частота обладает свойством устойчивости: в разных сериях из будущего числа испытаний относительные частоты приблизительно одинаковы. Значит, существует число, около которого они группируются. Отсюда получаем статистическое определение вероятности.
Число, около которого группируется относительные частоты события, соответствующие разным сериям из большого числа испытаний, называется вероятностью этого события. Точно узнать это число невозможно. Приближенно его можно заменить относительной частотой при большом числе испытаний.
Сложение вероятностей.
В этом и следующих заголовках приведены теоремы, позволяющие по известным вероятностям «простых» событий вычислять вероятности более сложных событий.
Суммой А + В событий А и В называются событие, состоящее в появлении хотя бы одного из них. Если событие А и В несовместны (т.е. не могут появится вместе в одном испытании), то их суммой будет появление одного из них, все равно какого.
Например, в ящике несколько красных, зеленых и бесцветных шаров. Наугад вынимают шар. Назовем событие А появление красного шара, событием В – зеленого. Тогда событием А + В будет появление любого цветного шара.
Теорема сложения вероятностей. Вероятность суммы несовместных событий равна сумме их вероятностей.
Р (А + В) = Р(А) + Р(В).
Пример. Мишень состоит из круга и охватывающего его кольца. Вероятность попасть в круг равна 0,2; в кольцо – 0,3. Найти вероятность поражения мишени.
Решение. Обозначим события: А – попадение в круг, В – попадение в кольцо. Поражение мишени – это событие А +В.
Р (А + В) = Р(А) + Р(В) = 0,2 + 0,3 = 0,5.
Противоположные события.
Два не совместных события называются противоположными, если в результате испытания какое-нибудь из них обязательно проявляется.
Событие, противоположное событию А, обозначается 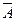 .
.
Например, А- попадение в цель, 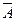 - промах.
- промах.
Теорема (свойство противоположных событий). Вероятности противоположных событий а сумме составляют единицу.
Р (А) + Р( 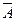 ) = 1
) = 1
Пример. Вероятность попадания в цель равна 0,8. Найти вероятность промаха.
Решение. 1 – 0,8 = 0,2.
Умножение вероятности.
Произведением АВ событий А и В называется событие, состоящее в появлении вместе.
Например. Если а- деталь годная, В – деталь окрашенная, то АВ – деталь и годная и окрашена.
События А и В называются НЕЗАВИСИМЫМИ, если появление или непоявление одного из них никак не отражается на появлении или непоявлении другого.
Теорема умножения вероятностей. Вероятность произведения независимых событий равна произведению их вероятностей.
Р (АВ) = Р(А) * Р(В).
Пример использование теоремы см. в разделе «Образец решения контрольной работы», задача 3.26, а.
2.2. Случайные величины.
Закон распределения дискретной, случайной величины.
Если для некоторой величины нельзя с точностью предсказать, какое значение она примет в результате испытания, то она называется СЛУЧАЙНОЙ.
Например, испытание – подбрасывание игральной кости, число выпадающих очков – случайная величина.
Случайные величины обозначаются прописными буквами Х, У, Z, ...., а принимаемые ими значения – соответствующими строчными буквами.
Если возможные значения случайной величины отделены одно от другого промежутками, то она называется ДИСКРЕТНОЙ. Например, число очков, выпадающих при подбрасывании игральной кости, - есть дискретная величина.
Закон распределение дискретной величины есть перечень всех ее возможных значений вместе с вероятностями их появления. Он оформляется в виде таблицы.

| Х | х1 х2 ...........хm |
| Р | р1 р2 ...........рm |
В верхней строке записывается значения случайной величины, в нижней – соответствующие вероятности.
Пример. В лотерее на каждые 100 билетов разыгрывается один выигрыш в 50 рублей и 10 выигрышей в 1 рубль. Составить закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного билета.
Решение.
| Х | 0 1 50 |
| Р | 89/100 10/100 1/100 |
Математическое ожидание дискретной,
случайной величины.
Математическим ожиданием М [x] дискретной случайной величины Х называться сумма произведений ее значений на соответствующие вероятности
М [x] = х1 р1 + х2 р2 + .........+ хm рm
Пример. Найти мат ожидание выигрыша на один билет в условиях примера из предыдущего пункта.
Решение.
М [x] = 0 * 89/100 + 1 * 10/100 + 50 * 1/100 = 0,6 рублей.
Устойчивость статистической средней.
Пусть проведено п испытаний, в которых случайная величина приняла п, раз значение х1, п2 раз значение х2 , ........, пm раз значение хm .
Средняя арифметическая из этих значений.
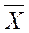 = (х1 п1 + х2 п2 + .......+ хm пm ) /п , называется СТАТИСТИЧЕСКОЙ СРЕДНЕЙ.
= (х1 п1 + х2 п2 + .......+ хm пm ) /п , называется СТАТИСТИЧЕСКОЙ СРЕДНЕЙ.
Теорема (свойство устойчивости статистической средней).
При большом числе испытаний статистическая средняя близка к матожиданию:
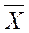 ≈ М [x]
≈ М [x]
(и тем ближе, чем больше испытаний).
Это свойство позволяет по известному ожиданию приблизительно предсказать статистическую среднюю и сумму значений случайной величины при заданном числе испытаний.
Пример. В условиях примера из предыдущего заголовка предсказать средний выигрыш на один билет и общую величину выигрыша для владельца двухсот билетов.
Решение. Средняя величина выигрыша на один из двухсот билетов
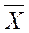 ≈ М [x] = 0,6 рублей
≈ М [x] = 0,6 рублей 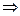
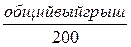 ≈ 0,6
≈ 0,6 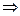 общий выигрыш ≈ 0,6 * 200 = 120 рублей.
общий выигрыш ≈ 0,6 * 200 = 120 рублей.
Дисперсия и среднеквадратическое отклонение
дискретной случайной величины.
Дисперсией Д [x] случайной величины Х называется число :
Д [x] = 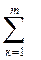 (хк - М [x])2 Рк
(хк - М [x])2 Рк
Среднеквадратическим отклонением σ [x] случайной величины Х называется квадратный корень из ее дисперсии:
σ [x] = 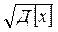
Пример вычисления дисперсии и среднеквадратического отклонения см. в разделе «Образец решения контрольной работы», задача 4.26. Д [x] и σ [x] служат мерой рассеяния значений случайной величины около ее ожидания.
Плотность распределения непрерывной
случайной величины.
Если возможные значения случайной величины сплошь заполняют некоторый промежуток [а, в], то она называется непрерывной.
Например. Некоторого маршрута отправляются каждые 45 мин. Время ожидания для пассажира, наугад пришедшего на остановку, есть непрерывная случайная величина со значениями в промежутке [0,45].
Пусть х- любое значение из [а, в]. Обозначим как Р(х < Х < х + Δх) вероятность того, что Х примет какое-нибудь значение в промежутке (х , х + Δх). Величина Р(х < Х < х + Δх)/ Δх есть средняя плотность вероятности на этом промежутке (вероятность, приходящаяся на единицу длины).
Предел средней плотности при стягивании промежутка (х, х + Δх) в точку х:
F(х) = 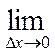
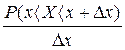 называется ПЛОТНОСТЬЮ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Х.
называется ПЛОТНОСТЬЮ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Х.
Зная плотность f(х), можно получить любое сведения о случайной величине (вычислить вероятность попадения в заданный промежуток, найти матожидание и др.).
Матожидание и дисперсия непрерывной
случайной величины.
Вычисляются по формулам:
М [x] = 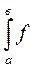 (х) х d х.
(х) х d х.
Д [x] = 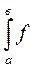 (х - М [x])2 f (х) d х.
(х - М [x])2 f (х) d х.
Пример. Непрерывная случайная величина Х распределена в промежутке [0,3] с плотностью f (х) = х2/9. Найти матожидание и дисперсию Х.
Решение.
М [x] = 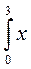 *
* 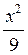 d х =
d х = 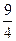 ,
,
Д [x] = 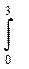 (х *
(х * 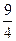 d х =
d х = 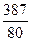 .
.
Вероятность попадания в заданный промежуток
(общий случай)
Вероятность Р(α < X < β), того, что непрерывная случайная величина Х примет какое-нибудь значение в заданном промежутке (α , β), вычисляется по формуле:
Р(α < X < β) = 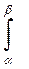 f (х) d х
f (х) d х
Пример. Для случайной величины из примера предыдущего подзаголовка найти вероятность попадания в промежуток (1.2).
Решение.
Р(1 < X < 2) = 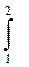
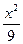 d х
d х 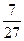 .
.
Нормальное распределение.
Если случайная величина Х может принимать любое значения, а ее плотность распределения есть:
f (х) = 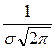 l-(х-а)2/ (2σ2), (σ> 0, а – любое)
l-(х-а)2/ (2σ2), (σ> 0, а – любое)
то она считается распределенной по нормальному закону..
используя формулы подзаголовка «Матожидание и дисперсия непрерывной случайной величины», найдем:
М [x] = а, σ [х] = σ.
Многие случайные величины распределены по нормальному закону. Среди них- ошибки измерений и отклонения размеров деталей от номинала.
Вероятность попадания в заданный промежуток
в случае нормального распределения.
Подставляя плотность нормального распределения в формулу:
Р(α < X < β) = 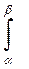 f (х) d х,
f (х) d х,
Получим: Р(α < X < β) = φ ( 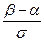 ) – φ (
) – φ ( 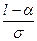 )
)
Здесь символ φ обозначает функцию: φ (Z) = 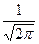
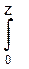 l-t2/2 dx,
l-t2/2 dx,
Называемую ФУНКЦИЕЙ ЛАПЛАСА. Ее значения находятся с помощью таблиц, которые имеются в учебниках теории вероятностей и в математических справочниках.
Если значения аргумента отрицательны, то для вычисления φ используются свойство ее нечетности.
Пример на применение формулы см. в разделе «Образец решения контрольной работы», задача 5.26.
Образец решения контрольной работы.
1.26. найти область сходимости степенного ряда: 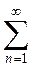
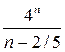 хп
хп
Решение. R = 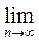
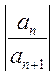 =
= 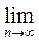
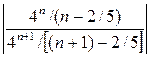 =
= 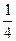
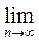
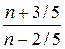 =
= 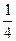
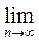
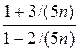 =
= 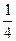
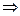
Интервал схождения есть - ¼ < x < 1/4 .
Проведем исследование на концах интервала сходимости. Подставим в ряд х = ¼. Получится числовой знакоположительный ряд 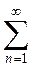
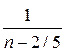 . Сравним его с гармоническим рядом
. Сравним его с гармоническим рядом 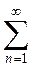
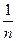 , который расходится
, который расходится
(р = 1): 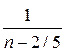
 >
> 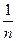
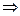 данный ряд также расходится х = ¼ не входит в область сходимости.
данный ряд также расходится х = ¼ не входит в область сходимости.
Подставим х=-1/4. Получится знакочередующий ряд 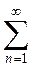
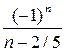 . Применим признак Лейбница:
. Применим признак Лейбница:
Величина 1/(п – 2/5) убывает с ростом п и 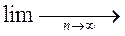
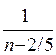 = 0
= 0 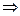 ряд сходится х = -1/4 входит в область сходимости.
ряд сходится х = -1/4 входит в область сходимости.
Итак, область сходимости есть -1/4 ≤ x < ¼.
2.26. С точностью до 0,001 вычислить интеграл 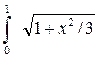 dх, разложив подинтегральную функцию в ряд Маклорена.
dх, разложив подинтегральную функцию в ряд Маклорена.
Решение.
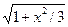 = (1 + Z)1/2 =
= (1 + Z)1/2 =
обозначим Z = 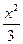 , применим биноминальный ряд при m = ½.
, применим биноминальный ряд при m = ½.
= 1 + 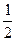 Z +
Z + 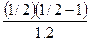 Z2 +
Z2 + 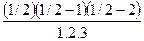 Z3 + ...... = 1 + (1/2) Z – (1/8) Z2
Z3 + ...... = 1 + (1/2) Z – (1/8) Z2
+ (1/16) Z3 - ... = 1 + (1/2) (х2/3) - (1/2) (х2/3)2 + (1/16) (х2/3)3 - ...= 1 + (1/6)х2 – (1/72)х4 + (1/432)х6 - ......
Это равенство справедливо при -1 < Z < 1 или при -1 < х2/3 < 1, т. е. при х2/3 < 1, или х2 < 3, или - 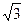 < х <
< х < 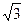 . Промежуток интегрирования 0 ≤ х ≤ 1 находится внутри этого интервала. Поэтому ряд можно подставить в интеграл вместо подинтегральной функции.
. Промежуток интегрирования 0 ≤ х ≤ 1 находится внутри этого интервала. Поэтому ряд можно подставить в интеграл вместо подинтегральной функции.
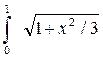 dх, =
dх, = 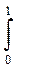 ( 1 +
( 1 + 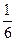 х2 -
х2 - 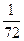 х4
х4  +
+ 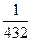 х6 - ......) d х =
х6 - ......) d х = 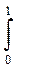 d х +
d х + 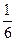
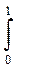 х2 d х -
х2 d х - 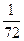
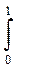 х4 d х +
х4 d х + 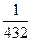
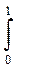 х6 d х - ...... = х
х6 d х - ...... = х 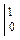 +
+ 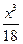
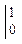 +
+ 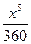
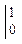 +
+ 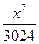
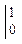 - ..... = 1 + 1/18 – 1/360 + 1/3024 -.... ≈ 1 + 0,05556 – 0,00278 + 0,00033 - .... ≈ 1 + 0,05556 – 0,00278 ≈ 1,053.
- ..... = 1 + 1/18 – 1/360 + 1/3024 -.... ≈ 1 + 0,05556 – 0,00278 + 0,00033 - .... ≈ 1 + 0,05556 – 0,00278 ≈ 1,053.
Мы отбросили члена начиная с четвертого, допустив погрешность, меньшую его абсолютной величины 0,00033, тем более меньшую, чем 0,001.
Итак, 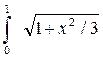 dх ≈ 1,053.
dх ≈ 1,053.
3.26. Два стрелка делают залп по цели. Первый попадает с вероятностью 0,9; второй – 0,8. Найти вероятность того что попадут а) оба; б) только один; в) хотя бы один.
Решение.
Обозначим события: А – первый попадет, В – второй попадет.
Тогда:
а) АВ – оба попадут. По теореме умножения вероятностей имеет: Р(АВ) = Р (А) * Р(В) = 0,9 * 0,8 = 0,72;
б) А 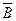 +
+ 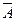 В – попадет только один ( либо первый попадет, второй нет; либо первый промахнется, второй попадет). По теореме сложения вероятностей получаем:
В – попадет только один ( либо первый попадет, второй нет; либо первый промахнется, второй попадет). По теореме сложения вероятностей получаем:
Р (А 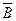 +
+ 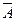 В) = Р (А
В) = Р (А 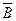 ) + Р (
) + Р ( 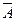 В) = Р(А) Р(
В) = Р(А) Р( 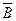 ) + Р(
) + Р( 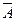 ) Р(
) Р( 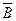 ) = 0,9 (1 – 0,8) + (1 – 0,9) * 0,8 = 0,26;
) = 0,9 (1 – 0,8) + (1 – 0,9) * 0,8 = 0,26;
В) обозначим как С событие, состоящее в ходя бы 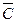 =
= 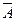
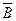 ,
,
Р(С) = 1 – Р( 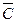 ) = 1 – Р(
) = 1 – Р( 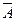
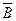 ) = 1 - Р(
) = 1 - Р( 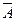 ) * Р(
) * Р( 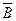 ) = 1 – (1 – 0,9) (1 – 0,8) = 0,98.
) = 1 – (1 – 0,9) (1 – 0,8) = 0,98.
4.26. Дан закон распределения дискретной случайной величины Х:
| Х | 1 2 5 |
| Р | 0,5 0,3 0,2 |
Найти матожидание, дисперсию и среднеквадратическое отклонение Х.
Решение.
М [Х] = х1 р1 + х2 р2 + х3 р3 = 1 * 0,5 + 2 * 0,3 + 5 * 0,2 = 2,1
Д [Х] = (х1 - М [Х] )2 р1 + (х2 - М [Х] )2 р2 + (х3 - М [Х] )2 р3 = (1 – 2,1)2 * 0,5 + (2 – 2,1)2 * 0,3 + (5 – 2,1)2 *0,2 = 2,29.
Σ [Х] = 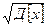 =
= 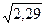 ≈ 1,513.
≈ 1,513.
5.26. Известны матожидания α = 2 и среднеквадратическое отклонение σ = 4 нормально распределенной случайной величины Х. Найти вероятность того, что Х примет какое –нибудь значение в промежутке (1.10).
Решение.
Применим формулу : Р(α < X < β) = Ф ( 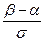 ) – Ф (
) – Ф ( 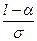 )
)
Р(1 < X < 10) = Ф ( 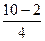 ) – Ф(
) – Ф( 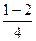 ) = Ф (2) – Ф (-0,25) = Ф (2) + φ (0,25)
) = Ф (2) – Ф (-0,25) = Ф (2) + φ (0,25)
≈ 0,4772 + 0,0987 = 0,5759.
Дата добавления: 2014-12-01; просмотров: 1227;
