СТЕПЕННЫЕ РЯДЫ.

Область сходимости функционального ряда.

Ряд f₁ (х) + f₂ (х) + f₃ (х) + .......+ f_п (х) + ....., членами которого являются функции, называется функциональным.

Если вместо переменной х подставить какое-либо конкретное значение, то все функции f_п (х) примут определенные числовые значения и ряд превратится в числовой. Подставляя вместо х разные числа, получим разные числовые ряды. Часть из них будут сходящимися, другие – расходящимися. Отсюда получаем определение: множество значений х, при подстановке которых в функциональный ряд получается сходящиеся числовые ряды, называется его областью сходимости.

Получающиеся при различных значениях х, взятых из области сходимости, числовые ряды будут различными и , значит, будут иметь различные суммы. Таким образом, сумма функционального ряда есть функция от х.

Степенной ряд.

Функциональный ряд вида а₀ + а₁х + а₂х² + а₃х³ + ....+ а_пх^п + а_п+1 х^п+1 +.

называется степенным.

(а₀, а₁, а₂, ........, а_п, .......... – постоянные коэффициенты).

Число R = 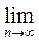|а_п/а_п+1 |

называется радиусом сходимости.

ТЕОРЕМА. Область сходимости степенного ряда состоит из интервала сходимости, -R < x < R и, может быть, одного или обоих его концов.

Пример на отыскание области сходимости см. в разделе «Образец решения контрольной работы», задача 1.26.