Ряд Маклорена.
Разложить данную функцию в степенной ряд – это, значит, найти такой степенной ряд, сумма которого совпадает с данной функцией во всех точках области сходимости.
В степенной ряд раскладывается не каждая функция. Но для всех практически важных функций, с которыми мы будем иметь дело, справедливо утверждение: если f (х) определена при х = 0 и имеет в этой точке производные любого порядка, то разложение возможно и имеет ряда Маклорена:
f (х) = f (0) + f'(0)х + 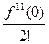 х2 +
х2 + 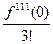 х3 +
х3 + 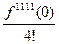 +
+
п! – читается «эн-факториал»; по определению;
п! = 1 * 2 * 3 * 4*.....* (п – 1) * п).
Пример. Разложить в ряд Маклорена функцию: f (х) = ln (1 + х)1
Дата добавления: 2014-12-01; просмотров: 996;
