II. РЯДЫ.

Числовые ряды.

Сходимость числового ряда

Пусть дана бесконечная последовательность чисел:

u ₁, u₂ , u₃ , u₄ ......... u_п ,.....

составим из них новую последовательность:

S₁ = u₁, S₂ = u₁ + u₂, S₃ = u₁ + u₂ + u₃,

S₄ = u₁ + u₂ + u₃ + u₄ ........,

S_п = u₁ + u₂ + u₃ + u₄ +.......+.u_п.

Процесс ее составления обозначают выражением:

u₁ + u₂ + u₃ + u₄ +.......+. u_п +...... = 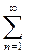u_п.

которое называется числовым рядом.

Числа u₁ , u₂ , u₃ , u₄ ,........... называются членами ряда.

п- ый член u_п называются также общим членом ряда.

Числа S₁, S₂, S₃, S₄ ,........ S_п,.......называются частичными суммами ряда.

Ряд называется сходящимся, если последовательность частичных сумм имеет конечный предел: 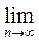S_п = S.

Этот предел называется суммой ряда.

Запись: u₁ + u₂ + u₃ + .......+.u_п + ... = S,

Означает, что ряд сходится и его сумма равна числу S.

Например, для ряда 0,9 + 0,09 + 0,009 + 0,0009 + ...последовательность частичных сумм.

S₁ = 0,9 , S₂ = 0,99, S₃ = 0,999, S₄ = 0,9999,.......

Имеет конечный предел 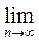S_п = 1, следовательно, ряд сходится и его сумма равна единице: 0,9 + 0,09 + 0,009 + 0,0009 +.... = 1.

Если последовательность частичных сумм не имеет предела или он бесконечен, то говоря, что ряд расходится.

Необходимое условие сходимости ряда.

В этом и следующих пунктах приведен ряд теорем, позволяющих устанавливать сходимость или расходимость ряда, не вычисляя предела последовательности частичных сумм.

ТЕОРЕМА. (необходимое условие сходимости).

Если ряд сходится, то его общий член стремится к нулю ( 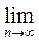u_п = 0).

Как следствие, получаем:

Если общий член не стремится к нулю, то ряд расходится.

Пример. Исследовать сходимость ряда (т.е. установить, сходится он или расходится)

2/1 + 3/2 + 4/3 + 5/4 + .....+ (п + 1)/п + ....

Решение:

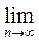
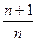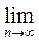= (1 + 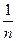) = 1 ≠ 0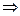

ряд расходится.

Признак Даламбера.

Пусть u₁ + u₂ + u₃ + .......+.u_п + u_{п +1} .......

знакоположительный ряд (все его члены положительны).

ТЕОРЕМА (признак Даламбера сходимости ряда)

Если 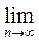(u_{п +1} / u_п) < 1 (> 1), то ряд сходится (расходится).

Пример.

Исследовать сходимость ряда: ½ + 2/4 + 3/8 + .....п/2^п + (п + 1) /2^п+1 +...

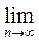
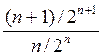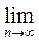
Решение: = = 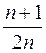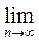( 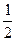+ 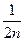) = 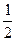< 1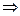

ряд сходится.

Гармонический ряд.

Ряд

1 + 1/2^р + 1/3^р + ..... + 1/п^р +......

называемый гармоническим, сходится (расходится) если р> 1 (р ≤ 1).

Сравнение рядов.

Пусть даны два знакоположительных ряда. Предположим, что каждый член одного из них не превосходит соответствующего члена другого.

ТЕОРЕМА (признак сравнения):

Если сходится ряд с большими членами, то и ряд с меньшими членами сходится.

Если расходится ряд с меньшими членами, то и ряд с большими членами расходится.

Теорема позволяет исследовать сходимость некоторых рядов, «сравнивая» их с рядами, с сходимости или расходимости которых уже известно.

Пример.

Исследовать сходимость ряда .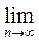

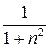Решение. Сравним данный ряд с гармоническим рядом 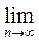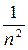, который сходится (р = 2 > 1): 1/ (1 + п²) <1 / п² 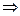данный ряд сходится.

Признак Лейбница.

Ряд а₁ – а₂ + а₃ –а₄ + ...+ (-1)^п+1 а_п +...... , где все числа а₁ , а₂ , а₃ ,

......., а_п ,..... положительны, называются знакочередующимся..

ТЕОРЕМА (признак Лейбница сходимости знакочередующегося ряда):

Если абсолютная величина общего члена а_п стремится к нулю и монотонно убывает, то ряд сходится.

Пример. Исследовать сходимость ряда

1 – ½ + 1/3 – ¼ + .....+ (-1)^п+1/п + .....

Решение. А_п = 1/п монотонно убывает с ростом п и 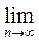(1/п) = 0 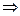ряд сходится.

Оценка погрешности приближенного вычисления

суммы знакочередующегося ряда.

Сумма всякого сходящегося ряда можно приближенно с любой степенью точности вычислить, заменив ее частичной суммой с достаточной большим номером (S ≈ S_п). При этом возникает вопрос об оценке погрешности.

Для ряда, удовлетворяющего условиям признака Лейбница, справедливо утверждение:

Погрешность меньше абсолютной величины первого отброшенного члена.

(| S – S | < а_п+1).

Пример. Для ряда, сходимость которого установлена в предыдущем пункте, найти сумму с точностью до 0,1,.

Решение:

S = 1 – ½ + 1/3 –..... + 1/9 – 1/10 +.....≈ 1 – ½ + 1/3 –.....+ 1/9 ≈ 1 – 0,5 + 0,333 – 0,25 + 0,2 – 0,167 + 0,143 – 0,125 + 0,111 ≈ 0,7.