Выделение мод движения тела как твердого целого

В ряде случаев геометрия конструкции имеет достаточно сложный характер, что делает затруднительным выявление возможных форм ее движения как жесткого целого. Моды движения конструкции как жесткого целого могут появиться в результате неправильного задания условий ее закрепления, что является распространенной ошибкой, совершаемой на этапе подготовки исходной информации.

Число мод (возможных способов) движения тела как жесткого целого можно определить на основе анализа матрицы жесткости. Сначала необходимо преобразовать матрицу жесткости к диагональному виду (к главным направлениям). Для этого следует определить ее собственные числа и собственные векторы. По определению вектор 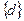, для которого становится возможным равенство

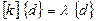(5.32)

называется собственным вектором матрицы, а соответствующее число 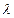- ее собственным числом. Равенство (5.39) эквивалентно однородной системе уравнений

, (5.33)

которая, как известно, имеет ненулевое решение лишь при условии, что ее определитель равен нулю. Получаем характеристическое уравнение для матрицы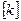

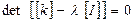, (5.34)

которое представляет собой алгебраическое уравнение n-й степени. Корни этого уравнения являются собственными значениями матрицы 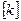. Каждому собственному значению 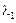соответствует ненулевой вектор , удовлетворяющий равенству 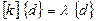, называемый собственным вектором.

После определения собственных чисел и собственных векторов матрицы 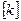становится возможным с помощью преобразования системы координат привести ее к так называемому «модальному» виду, при котором она становится диагональной. Диагональные компоненты модальной матрицы 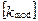будут равны найденным собственным числам. Очевидно, что число независимых уравнений в 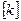определяется ненулевыми компонентами в модальной матрице жесткости 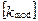. Число нулевых диагональных элементов даст число возможных движений тела как жесткого целого. Так как диагональные элемента модальной матрицы являются собственными числами, то поиск числа мод движений тела как жесткого целого сводится к нахождению нулевых корней характеристического уравнения (5.34).