Преобразование степеней свободы

Пусть для некоторого вектора 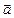(рис. 5.11) компоненты, заданные в одной системе координат матрицей-столбцом надо вычислить в другой системе координат, представив столбцом . Указанное преобразование можно выполнить с помощью операции

(5.22)

Рис. 5.11

Так, например, для преобразования компонент вектора из одной плоской системы декартовых координат в другую, полученную с помощью поворота исходной системы координат, матрица 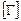должна быть сформирована следующим образом

. (5.23)

Преобразование координат в случае ортогональных осей обладает свойством . По определению обратной матрицы 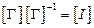. Поэтому должно иметь место равенство

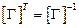. (5.24)

Матрицы, для которых обратная матрица равна транспонированной, называются ортогональными.

Предположим, что уравнения жесткости элемента

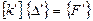, (5.25)

сформированные в локальной системе координат надо преобразовать к глобальной системе координат.

Для векторов, относящихся к произвольному узлу p элемента в соответствии с (5.22) можно записать

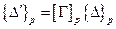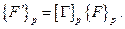, (5.26)

Если весь элемент содержит m узлов, то матрица преобразования для всего элемента будет иметь блочно-диагональный вид

(5.27)

Тогда степени свободы и узловые силы всего конечного элемента преобразуются по правилу

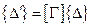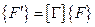, . (5.28)

Подставляя (5.28) в уравнения жесткости элемента (5.25), получим равенство

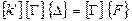. (5.29)

После умножения на 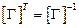левой и правой части (5.29) получим

. (5.30)

То есть матрица жесткости при переходе в другую систему координат будет преобразовываться по закону

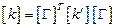. (5.31)

Поскольку при использовании преобразования (5.31) нет необходимости обращать матрицу [Г], а надо ее только транспонировать, то она не обязательно должна быть квадратной. Следовательно, возможен переход из пространства n измерений в пространство m измерений. Например, матрица жесткости стержневого элемента (5.5), сформированная для одномерного случая, может быть преобразована в плоскую или пространственную систему координат.