Максвелл ввел понятие полного тока,равного сумме токов проводимости (а также конвекционных токов) и смещения.Плотность полного тока 12 страница

§ 196. Вращение плоскости поляризации

Некоторые вещества (например, из твердых тел — кварц, сахар, киноварь, из жид­костей — водный раствор сахара, винная кислота, скипидар), называемыеоптически активными, обладают способностью вращать плоскость поляризации.

Вращение плоскости поляризации можно наблюдать на следующем опыте (рис. 285). Если между скрещенными поляризатором Р и анализатором А, дающими темное поле зрения, поместить оптически активное вещество (например, кювету с раствором сахара), то поле зрения анализатора просветляется. При повороте анализатора на некоторый угол j можно вновь получить темное поле зрения. Угол j и есть угол, на который оптически активное вещество поворачивает плоскость поляризации света, прошедшего через поляризатор. Так как поворотом анализатора можно получить темное поле зрения, то свет, прошедший через оптически активное вещество, является плоскополяризованным.

Опыт показывает, что угол поворота плоскости поляризации для оптически актив­ных кристаллов и чистых жидкостей

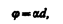
для оптически активных растворов

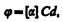(196.1)

где d — расстояние, пройденное светом в оптически активном веществе, a([a]) — так называемое удельное вращение, численно равное углу поворота плоскости поляризации света слоем оптически активного вещества единичной толщины (единичной концент­рации — для растворов), С — массовая концентрация оптически активного вещества в растворе, кг/м³. Удельное вращение зависит от природы вещества, температуры и длины волны света в вакууме.

Опыт показывает, что все вещества, оптически активные в жидком состоянии, обладают таким же свойством и в кристаллическом состоянии. Однако если вещества активны в кристаллическом состоянии, то не всегда активны в жидком (например, расплавленный кварц). Следовательно, оптическая активность обусловливается как строением молекул вещества (их асимметрией), так и особенностями расположения частиц в кристаллической решетке.

Оптически активные вещества в зависимости от направления вращения плоскости поляризации разделяются на право- и левовращающие. В первом случае плоскость поляризации, если смотреть навстречу лучу, вращается вправо (по часовой стрелке), во втором — влево (против часовой стрелки). Вращение плоскости поляризации объяс­нено О. Френелем (1817 г.). Согласно теории Френеля, скорость распространения света в оптически активных веществах различна для лучей, поляризованных по кругу вправо и влево.

Явление вращения плоскости поляризации и, в частности, формула (196.1) лежат в основе точного метода определения концентрации растворов оптически активных веществ, называемого поляриметрией (сахариметрией). Для этого используется установ­ка, показанная на рис. 285. По найденному углу поворота плоскости поляризации j и известному значению [a] из (196.1) находится концентрация растворенного вещества.

Впоследствии М. Фарадеем было обнаружено вращение плоскости поляризации в оптически неактивных телах, возникающее под действием магнитного поля. Это явление получило название эффект Фарадея (или магнитного вращения плоскости поляризации). Оно имело огромное значение для науки, так как было первым явлением, в котором обнаружилась связь между оптическими и электромагнитными процессами.

Глава 26 Квантовая природа излучения

§ 197. Тепловое излучение и его характеристики

Тела, нагретые до достаточно высоких температур, светятся. Свечение тел, обусловлен­ное нагреванием, называется тепловым (температурным) излучением. Тепловое излуче­ние, являясь самым распространенным в природе, совершается за счет энергии тепло­вого движения атомов и молекул вещества (т. е. за счет его внутренней энергии) и свойственно всем телам при температуре выше 0 К. Тепловое излучение характеризу­ется сплошным спектром, положение максимума которого зависит от температуры. При высоких температурах излучаются короткие (видимые и ультрафиолетовые) элект­ромагнитные волны, при низких — преимущественно длинные (инфракрасные).

Тепловое излучение — практически единственный вид излучения, который может быть равновесным. Предположим, что нагретое (излучающее) тело помещено в по­лость, ограниченную идеально отражающей оболочкой. С течением времени, в резуль­тате непрерывного обмена энергией между телом и излучением, наступит равновесие, т. е. тело в единицу времени будет поглощать столько же энергии, сколько и излучать. Допустим, что равновесие между телом и излучением по какой-либо причине нарушено и тело излучает энергии больше, чем поглощает. Если в единицу времени тело больше излучает, чем поглощает (или наоборот), то температура тела начнет понижаться (или повышаться). В результате будет ослабляться (или возрастать) количество излучаемой телом энергии, пока, наконец, не установится равновесие. Все другие виды излучения неравновесны.

Количественной характеристикой теплового излучения служит спектральная плот­ность энергетической светимости (излучательности) тела — мощность излучения с еди­ницы площади поверхности тела в интервале частот единичной ширины:

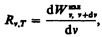
где d 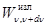— энергия электромагнитного излучения, испускаемого за единицу време­ни (мощность излучения) с единицы площади поверхности тела в интервале частот от n до n+dn.

Единица спектральной плотности энергетической светимости (R_n,T) —джоуль на метр в квадрате (Дж/м²).

Записанную формулу можно представить в виде функции длины волны:

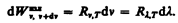
Так как c=ln, то

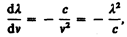
где знак минус указывает на то, что с возрастанием одной из величин (n или l) другая величина убывает. Поэтому в дальнейшем знак минус будем опускать. Таким образом,

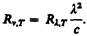(197.1)

С помощью формулы (197.1) можно перейти от R_n,T к R_l,T и наоборот.

Зная спектральную плотность энергетической светимости, можно вычислить интег­ральную энергетическую светимость (интегральную излучательность) (ее называют про­сто энергетической светимостью тела), просуммировав по всем частотам:

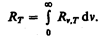(197.2)

Способность тел поглощать падающее на них излучение характеризуется спект­ральной поглощательной способностью

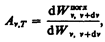
показывающей, какая доля энергии, приносимой за единицу времени на единицу площади поверхности тела падающими на нее электромагнитными волнами с частота­ми от n до n+dn, поглощается телом. Спектральная поглощательная способ­ность — величина безразмерная. Величины R_n,T и А_n,T зависят от природы тела, его термодинамической температуры и при этом различаются для излучений с различными частотами. Поэтому эти величины относят к определенным Т и n (вернее, к достаточно узкому интервалу частот от n до n+dn).

Тело, способное поглощать полностью при любой температуре все падающее на него излучение любой частоты, называется черным. Следовательно, спектральная поглощательная способность черного тела для всех частот и температур тождественно равна единице ( 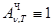). Абсолютно черных тел в природе нет, однако такие тела, как сажа, платиновая чернь, черный бархат и некоторые другие, в определенном интервале частот по своим свойствам близки к ним.

Идеальной моделью черного тела является замкнутая полость с небольшим отвер­стием О, внутренняя поверхность которой зачернена (рис. 286). Луч света, попавший внутрь такой полости, испытывает многократные отражения от стенок, в результате чего интенсивность вышедшего излучения оказывается практически равной нулю. Опыт показывает, что при размере отверстия, меньшего 0,1 диаметра полости, пада­ющее излучение всех частот полностью поглощается. Вследствие этого открытые окна домов со стороны улицы кажутся черными, хотя внутри комнат достаточно светло из-за отражения света от стен.

Наряду с понятием черного тела используют понятие серого тела — тела, поглощательная способность которого меньше единицы, но одинакова для всех частот и зави­сит только от температуры, материала и состояния поверхности тела. Таким образом, для серого тела 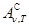=A_T = const<l.

Исследование теплового излучения сыграло важную роль в создании квантовой теории света, поэтому необходимо рассмотреть законы, которым оно подчиняется.

§ 188. Закон Кирхгофа

Кирхгоф, опираясь на второй закон термодинамики и анализируя условия равновес­ного излучения в изолированной системе тел, установил количественную связь между спектральной плотностью энергетической светимости и спектральной поглощательной способностью тел. Отношение спектральной плотности энергетической светимости к спектральной поглощательной способности не зависит от природы тела; оно является для всех тел универсальной функцией частоты (длины волны) и температуры (закон Кирхгофа):

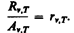(198.1)

Для черного тела 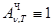, поэтому из закона Кирхгофа (см. (198.1)) вытекает, что R_n,T для черного тела равна r_n,T. Таким образом,универсальная функция Кирхгофа r_n,T есть не что иное,как спектральная плотность энергетической светимости черного тела. Следовательно, согласно закону Кирхгофа, для всех тел отношение спектральной плотности энергетической светимости к спектральной поглощательной способности равно спектральной плотности энергетической светимости черного тела при той же температуре и частоте.

Из закона Кирхгофа следует, что спектральная плотность энергетической светимо­сти любого тела в любой области спектра всегда меньше спектральной плотности энергетической светимости черного тела (при тех же значениях Т и n), так как А_n,T< 1 и поэтому R_n,T <r_n,T. Кроме того, из (198.1) вытекает, что если тело при данной температуре Т не поглощает электромагнитные волны в интервале частот от n до n+dn, то оно их в этом интервале частот при температуре T и не излучает, так как при А_n,T =0

R_n,T =0.

Используя закон Кирхгофа, выражение для энергетической светимости тела (197.2) можно записать в виде

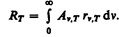
Для серого тела

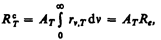(198.2)

где

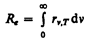
— энергетически светимость черного тела (зависит только от температуры).

Закон Кирхгофа описывает только тепловое излучение, являясь настолько харак­терным для него, что может служить надежным критерием для определения природы излучения. Излучение, которое закону Кирхгофа не подчиняется, не является тепловым.

§ 199. Законы Стефана — Больцмана и смещения Вина

Из закона Кирхгофа (см. (198.1)) следует, что спектральная плотность энергетическое светимости черного тела является универсальное функцией, поэтому нахождение ее явной зависимости от частоты и температуры является важной задачей теории тепло­вого излучения.

Австрийский физик И. Стефан (1835—1893), анализируя экспериментальные дан­ные (1879), и Л. Больцман, применяя термодинамический метод (1884), решили эту задачу лишь частично, установив зависимость энергетической светимости R_e от тем­пературы. Согласно закону Стефана — Больцмана,

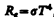(199.1)

т.е. энергетическая светимость черного тела пропорциональна четвертой степени его термодинамической температуры; s — постоянная Стефана — Больцмана: ее экспери­ментальное значение равно 5,67×10^–8 Вт/(м² × К⁴).

Закон Стефана — Больцмана, определяя зависимость R_е от температуры, не дает ответа относительно спектрального состава излучения черного тела. Из эксперимен­тальных кривых зависимости функции r_l,T от длины волны l 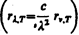при различных температурах (рис. 287) следует, что распределение энергии в спектре черного тела является неравномерным. Все кривые имеют явно выраженный максимум, который по мере повышения температуры смещается в сторону более коротких волн. Площадь, ограниченная кривой зависимости r_l,T от l и осью абсцисс, пропорциональна энер­гетической светимости R_e черного тела и, следовательно, по закону Стефана — Больц­мана, четвертой степени температуры.

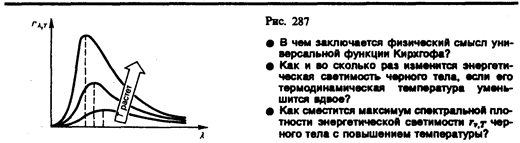
Немецкий физик В. Вин (1864—1928), опираясь на законы термо- и электродинами­ки, установил зависимость длины волны l_max, соответствующей максимуму функции r_l,T, от температуры Т. Согласно закону смещения Вина,

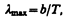(199.2)

т. е. длина волны l_max, соответствующая максимальному значению спектральной плотности энергетической светимости r_l,T черного тела, обратно пропорциональна его термодинамической температуре, b — постоянная Вина; ее экспериментальное значе­ние равно 2,9×10^–3 м×К. Выражение (199.2) потому называют законом смещения Вина, что оно показывает смещение положения максимума функции r_l,T по мере возрастания температуры в область коротких длин волн. Закон Вина объясняет, почему при понижении температуры нагретых тел в их спектре все сильнее преобладает длинновол­новое излучение (например, переход белого каления в красное при остывании металла).

§ 200. Формулы Рэлея — Джинса и Планка

Из рассмотрения законов Стефана — Больцмана и Вина следует, что термодинамичес­кий подход к решению задача о нахождении универсальной функции Кирхгофа r_n,T не дал желаемых результатов. Следующая строгая попытка теоретического вывода зави­симости r_n,T принадлежит английским ученым Д. Рэлею и Д. Джинсу (1877—1946), которые применили к тепловому излучению методы статистической физики, восполь­зовавшись классическим законом равномерного распределения энергии по степеням свободы.

Формула Рэлея — Джинса для спектральной плотности энергетической светимости черного тела имеет вид

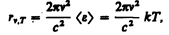(200.1)

где áeñ=kT — средняя энергия осциллятора с собственной частотой n. Для осцил­лятора, совершающего колебания, средние значения кинетической и потенциальной энергий одинаковы (см. § 50), поэтому средняя энергия каждой колебательной степени свободы áeñ=kT .

Как показал опыт, выражение (200.1) согласуется с экспериментальными данными только в области достаточно малых частот и больших температур. В области больших частот формула Рэлея — Джинса резко расходится с экспериментом, а также с законом смещения Вина (рис. 288). Кроме того, оказалось, что попытка получить закон Стефа­на — Больцмана (см. (199.1)) из формулы Рэлея — Джинса приводит к абсурду. Дейст­вительно, вычисленная с использованием (200.1) энергетическая светимость черного тела (см. (198.3))

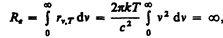
в то времякак по закону Стефана — Больцмана R_е пропорциональна четвертой степени температуры. Этот результат получил название «ультрафиолетовой катаст­рофы». Таким образом, в рамках классической физики не удалось объяснить законы распределения энергии в спектре черного тела.

В области больших частот хорошее согласие с опытом дает формула Вина (закон излучения Вина), полученная им из общих теоретических соображений:

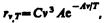
где r_n,T —спектральная плотность энергетической светимости черного тела, С и А — постоянные величины. В современных обозначениях с использованием постоянной Планка, которая в то время еще не была известна, закон излучения Вина может быть записан в виде

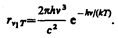
Правильное, согласующееся с опытными данными выражение для спектральной плотности энергетической светимости черного тела было найдено в 1900 г. немецким физиком М. Планком. Для этого ему пришлось отказаться от установившегося поло­жения классической физики, согласно которому энергия любой системы может изме­няться непрерывно, т. е. может принимать любые сколь угодно близкие значения. Согласно выдвинутой Планком квантовой гипотезе, атомные осцилляторы излучают энергию не непрерывно, а определенными порциями — квантами, причем энергия кванта пропорциональна частоте колебания (см. (170.3)):

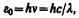(200.2)

где h= 6,625×10^–34 Дж×с —постоянная Планка. Так как излучение испускается порци­ями, то энергия осциллятора e может принимать лишь определенные дискретные значения, кратные целому числу элементарных порций энергии e₀:

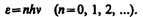
В данном случае среднюю энергию áeñ осциллятора нельзя принимать равной kT. В приближении, что распределение осцилляторов по возможным дискретным состояниям подчиняется распределению Больцмана (§ 45), средняя энергия осциллятора

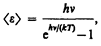
а спектральная плотность энергетической светимости черного тела

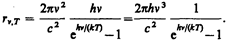
Таким образом, Планк вывел для универсальной функции Кирхгофа формулу

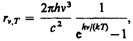(200.3)

которая блестяще согласуется с экспериментальными данными по распределению энергии в спектрах излучения черного тела во всем интервале частот и температур. Теоретический вывод этой формулы М. Планк изложил 14 декабря 1900 г. на заседа­нии Немецкого физического общества. Этот день стал датой рождения квантовой физики.

В области малых частот, т. е. при hn<<kT (энергия кванта очень мала по сравнению с энергией теплового движения kT), формула Планка (200.3) совпадает с формулой Рэлея — Джинса (200.1). Для доказательства этого разложим экспоненциальную функцию в ряд, ограничившись для рассматриваемого случая двумя первыми членами:

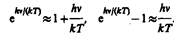
Подставляя последнее выражение в формулу Планка (200.3), найдем, что

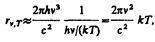
т. е. получили формулу Рэлея — Джинса (200.1).

Из формулы Планка можно получить закон Стефана—Больцмана. Согласно (198.3) и (200.3),

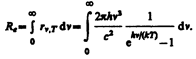
Введем безразмерную переменную x=hn/(kt); dx=hdn/(kT); dn=kTdx/h. Формула для R_e преоб­разуется к виду

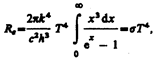(200.4)

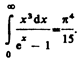где так как Таким образом, действительно формула Планка позволяет получить закон Стефана — Больцмана (ср. формулы (199.1) и (200.4)). Кроме того, подстановка числовых значений k, с и h дает для постоянной Стефана — Больцмана значение, хорошо согласующееся с экспериментальными данными. Закон смещения Вина получим с помощью формул (197.1) и (200.3):

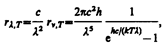
откуда

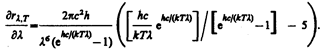
Значение l_max, при котором функция достигает максимума, найдем, приравняв нулю эту произ­водную. Тогда, введя x=hc/(kTl_max), получим уравнение

Решение этого трансцендентного уравнения методом последовательных приближений дает x=4,965. Следовательно, hc/(kTl_max)=4,965, откуда

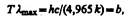
т. е. получили закон смещения Вина (см. (199.2)).

Из формулы Планка, зная универсальные постоянные h, k и с, можно вычислить постоянные Стефана — Больцмана s и Вина b. С другой стороны, зная эксперимен­тальные значения s и b, можно вычислить значения h и k (именно так и было впервые найдено числовое значение постоянной Планка).

Таким образом, формула Планка не только хорошо согласуется с эксперименталь­ными данными, но и содержит в себе частные законы теплового излучения, а также позволяет вычислить постоянные в законах теплового излучения. Следовательно, формула Планка является полным решением основной задачи теплового излучения, поставленной Кирхгофом. Ее решение стало возможным лишь благодаря революцион­ной квантовой гипотезе Планка.

§ 201. Оптическая пирометрия. Тепловые источники света

Законы теплового излучения используются для измерения температуры раскаленных и самосветящихся тел (например, звезд). Методы измерения высоких температур, использующие зависимость спектральной плотности энергетической светимости или интегральной энергетической светимости тел от температуры, называются оптической пирометрией. Приборы для измерения температуры нагретых тел по интенсивности их теплового излучения в оптическом диапазоне спектра называются пирометрами. В зави­симости от того, какой закон теплового излучения используется при измерении тем­пературы тел, различают радиационную, цветовую и яркостную температуры.

1. Радиационная температура — это такая температура черного тела, при которой его энергетическая светимость R_e (см. (198.3)) равна энергетической светимости R_T (см. (197.2)) исследуемого тела. В данном случае регистрируется энергетическая светимость исследуемого тела и по закону Стефана — Больцмана (199.1) вычисляется его радиаци­онная температура:

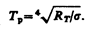
Радиационная температура T_р тела всегда меньше его истинной температуры Т. Для доказательства этого предположим, что исследуемое тело является серым. Тогда, используя (199.1) и (198.2), можно записать

С другой стороны,

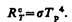
Из сравнения этих выражений вытекает, что

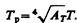
Так как А_T< 1, то T_р< T, т. е. истинная температура тела всегда выше радиационной.

2. Цветовая температура. Для серых тел (или тел, близких к ним по свойствам) спектральная плотность энергетической светимости

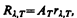
где A_T=const<1. Следовательно, распределение энергии в спектре излучения серого тела такое же, как и в спектре черного тела, имеющего ту же температуру, поэтому к серым телам применим закон смещения Вина (см. (199.2)). Зная длину волны l_max, соответствующую максимальной спектральной плотности энергетической светимости R_l,T исследуемого тела, можно определить его температуру

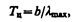
которая называется цветовой температурой. Для серых тел цветовая температура совпадает с истинной. Для тел, которые сильно отличаются от серых (например, обладающих селективным поглощением), понятие цветовой температуры теряет смысл. Таким способом определяется температура на поверхности Солнца (T_ц»6500 К) и звезд.

3. Яркостная температуря Т_я —это температура черного тела, при которой для определенной длины волны его спектральная плотность энергетической светимости равна спектральной плотности энергетической светимости исследуемого тела, т. е.

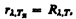(201.1)

где Т— истинная температура тела. По закону Кирхгофа (см. (198.1)), для исследу­емого тела при длине волны l

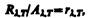(201.2)

или, учитывая (201.1),

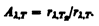
Taк как для нечерных тел А<1, то r_l,Tя<r_l,T и, следовательно, T_я<Т, т. е. истинная температура тела всегда выше яркостной.

В качестве яркостного пирометра обычно используется пирометр с исчезающей нитью. Накал нити пирометра подбирается таким, чтобы выполнялось условие (201.1). В данном случае изображение нити пирометра становится неразличимым на фоне поверхности раскаленного тела, т. е. нить как бы «исчезает». Используя проградуированный по черному телу миллиамперметр, можно определить яркостную тем­пературу.

Зная поглощательную способность А_l,Т тела при той же длине волны, по яркостной температуре можно определить истинную. Переписав формулу Планка (200.3) в виде

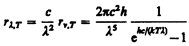
и учитывая это в (201.2), получим

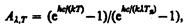
т. е. при известных А_l,Т и l можно определить истинную температуру исследуемого тела.

4. Тепловые источники света. Свечение раскаленных тел используется для создания источников света, первые из которых — лампы накаливания и дуговые лампы — были соответственно изобретены русскими учеными Л. Н. Лодыгиным в 1873 г. и П. Н. Яблочковым в 1876 г.

На первый взгляд кажется, что черные тела должны быть наилучшими тепловыми источниками света, так как их спектральная плотность энергетической светимости для любой длины волны больше спектральной плотности энергетической светимости нечерных тел, взятых при одинаковых температурах. Однако оказывается, что для некоторых тел (например, вольфрама), обладающих селективностью теплового излуче­ния, доля энергии, приходящаяся на излучение в видимой области спектра, значительно больше, чем для черного тела, нагретого до той же температуры. Поэтому вольфрам, обладая еще и высокой температурой плавления, является наилучшим материалом для изготовления нитей ламп.

Температура вольфрамовой нити в вакуумных лампах не должна превышать 2450 К, поскольку при более высоких температурах происходит ее сильное распыление. Максимум излучения при этой температуре соответствует длине волны »1,1 мкм, т. е. очень далек от максимума чувствительности человеческого глаза (»0,55 мкм). Напол­нение баллонов ламп инертными газами (например, смесью криптона и ксенона с добавлением азота) при давлении »50 кПа позволяет увеличить температуру нити до 3000 К, что приводит к улучшению спектрального состава излучения. Однако светоотдача при этом не увеличивается, так как возникают дополнительные потери энергии из-за теплообмена между нитью и газом вследствие теплопроводности и кон­векции. Для уменьшения потерь энергии за счет теплообмена и повышения светоотдачи газонаполненных ламп нить изготовляют в виде спирали, отдельные витки которой обогревают друг друга. При высокой температуре вокруг этой спирали образуется неподвижный слой газа и исключается теплообмен вследствие конвекции. Энергетичес­кий к.п.д. ламп накаливания в настоящее время не превосходит 5%.