Максвелл ввел понятие полного тока,равного сумме токов проводимости (а также конвекционных токов) и смещения.Плотность полного тока 11 страница

Свет представляет собой суммарное электромагнитное излучение множества атомов. Атомы же излучают световые волны независимо друг от друга, поэтому световая волна, излучаемая телом в целом, характеризуется всевозможными равнове­роятными колебаниями светового вектора (рис. 272, а; луч перпендикулярен плоскости рисунка). В данном случае равномерное распределение векторов Е объясняется боль­шим числом атомарных излучателей, а равенство амплитудных значений векторов Е — одинаковой (в среднем) интенсивностью излучения каждого из атомов. Свет со всевозможными равновероятными ориентациями вектора Е (и, следовательно, Н) называется естественным.

Свет, в котором направления колебаний светового вектора каким-то образом упорядочены, называется поляризованным. Так, если в результате каких-либо внешних воздействий появляется преимущественное (но не исключительное!) направление коле­баний вектора Е (рис. 272, б),то имеем дело с частично поляризованным светом. Свет, в котором вектор Е (и, следовательно, Н) колеблется только в одном направлении, перпендикулярном лучу (рис. 272, в), называется плоскополяризованным (линейно поляризованным).

Плоскость, проходящая через направление колебаний светового вектора плоскополяризованной волны и направление распространения этой волны, называется плоско­стью поляризации. Плоскополяризованный свет является предельным случаем эллиптически поляризованного света — света, для которого вектор Е (вектор Н) изменяется со временем так, что его конец описывает эллипс, лежащий в плоскости, перпен­дикулярной лучу. Если эллипс поляризации вырождается (см. § 145) в прямую (при разности фаз j, равной нулю или p), то имеем дело с рассмотренным выше плоскополяризованным светом, если в окружность (при j = ±p/2 и равенстве амплитуд склады­ваемых волн), то имеем дело с циркулярно поляризованным (поляризованным по кругу) светом.

Степенью поляризации называется величина

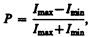
где I_max, и I_min — соответственно максимальная и минимальная интенсивности частично поляризованного света, пропускаемого анализатором. Для естественного света I_max=I_min и Р=0, для плоскополяризованного I_min =0 и Р=1.

Естественный свет можно преобразовать в плоскополяризованный, используя так называемые поляризаторы, пропускающие колебания только определенного направле­ния (например, пропускающие колебания, параллельные главной плоскости поляриза­тора, и полностью задерживающие колебания, перпендикулярные этой плоскости). В качестве поляризаторов могут быть использованы среды, анизотропные в отношении колебаний вектора Е, например кристаллы (их анизотропия известна, см. § 70). Из природных кристаллов, давно используемых в качестве поляризатора, следует от­метить турмалин.

Рассмотрим классические опыты с турмалином (рис. 273). Направим естественный свет перпендикулярно пластинке турмалина T₁, вырезанной параллельно так называ­емой оптической оси ОО' (см. § 192). Вращая кристалл T₁ вокруг направления луча, никаких изменений интенсивности прошедшего через турмалин света не наблюдаем. Если на пути луча поставить вторую пластинку турмалина T₂ и вращать ее вокруг направления луча, то интенсивность света, прошедшего через пластинки, меняется в зависимости от угла к между оптическими осями кристалловпо закону Малюса*:

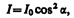(190.1)

где I₀ и I — соответственно интенсивности света, падающего на второй кристалл и вышедшего из него.

* Э. Малюс (1775—1812) — французский физик.

Следовательно, интенсивность прошедшего через пластинки света изменится от минимума (полное гашение света) при a=p/2 (оптические оси пластинок перпендикулярны) да максимума при a=0 (оптические оси пластинок парал­лельны). Однако, как это следует из рис. 274, амплитуда Е световых колебаний, прошедших через пластинку Т₂, будет меньше амплитуды световых колебаний Е₀, падающих на пластинку T₂.

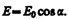
Так как интенсивность света пропорциональна квадрату амплитуды, то и получается выражение (190.1).

Результаты опытов с кристаллами турмалина объясняются довольно просто, если исходить из изложенных выше условий пропускания света поляризатором. Первая пластинка турмалина пропускает колебания только определенного направления (на рис. 273 это направление показано стрелкой AВ), т. е. преобразует естественный свет в плоскополяризованный. Вторая же пластинка турмалина в зависимости от ее ориен­тации из поляризованного света пропускает большую или меньшую его часть, которая соответствует компоненту Е, параллельному оси второго турмалина. На рис. 273 обе пластинки расположены так, что направления пропускаемых ими колебаний АВ и А'В' перпендикулярны друг другу. В данном случае Т₁ пропускает колебания, направленные по АВ, а Т₂ их полностью гасит, т.е. за вторую пластинку турмалина свет не проходит.

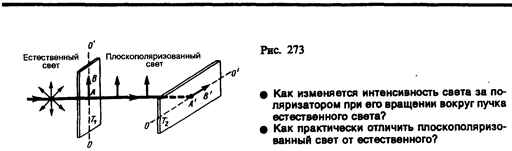
Пластинка Т₁, преобразующая естественный свет в плоскополяризованный, являет­сяполяризатором. Пластинка Т₂, служащая для анализа степени поляризации света, называется анализатором. Обе пластинки совершенно одинаковы (их можно поменять местами).

Если пропустить естественный свет через два поляризатора, главные плоскости которых образуют угол a, то из первого выйдет плоскополяризованный свет, интенсив­ность которого I₀=¹/₂I_ест, из второго, согласно (190.1), выйдет свет интенсивностью I=I₀cos²a . Следовательно, интенсивность света, прошедшего через два поляризатора,

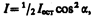
откуда I₀=¹/₂I_ест (поляризаторы параллельны) и I_min = 0 (поляризаторы скрещены).

§ 191. Поляризация света при отражении и преломлении на границе двух диэлектриков

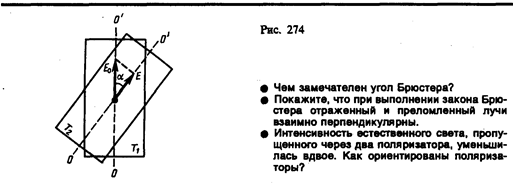
Если естественный свет падает на границу раздела двух диэлектриков (например, воздуха и стекла), то часть его отражается, а часть преломляется в распространяется во второй среде. Устанавливая на пути отраженного и преломленного лучей анализатор (например, турмалин), убеждаемся в том, что отраженный и преломленный лучи частично поляризованы: при поворачивании анализатора вокруг лучей интенсивность света периодически усаливается и ослабевает (полного гашения не наблюдается!). Дальнейшие исследования показали, что в отраженном луче преобладают колебания, перпендикулярные плоскости падения (на рис. 275 они обозначены точками), в прелом­ленном — колебания, параллельные плоскости падения (изображены стрелками).

Степень поляризации (степень выделения световых волн с определенной ориентаци­ей электрического (и магнитного) вектора) зависит от угла падения лучей и показателя преломления. Шотландский физик Д. Брюстер (1781—1868) установил закон, согласно которому при угле падения i_B (угол Брюстера), определяемого соотношением

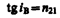
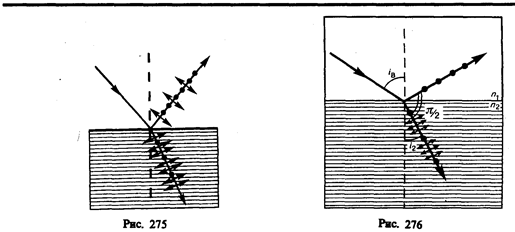
(n₂₁ — показатель преломления второй среды относительно первой), отраженный луч является плоскополяризованным (содержит только колебания, перпендикулярные плос­кости падения) (рис. 276). Преломленный же луч при угле падения i_B поляризуется максимально, но не полностью.

Если свет падает на границу раздела под углом Брюстера, то отраженный и прело­мленный лучи взаимно перпендикулярны (tgi_B = sini_B/cosi_B, n₂₁=sini_B/sini₂(i₂ — угол преломления), откуда cosi_B=sini₂). Следовательно, i_B + i₂ = p/2, но i’_B = i_B (закон от­ражения), поэтому i’_B + i₂ = p/2.

Степень поляризации отраженного и преломленного света при различных углах падения можно рассчитать из уравнений Максвелла, если учесть граничные условия для электромагнитного поля на границе раздела двух изотропных диэлектриков (так называемыеформулы Френеля).

Степень поляризации преломленного света может быть значительно повышена (многократным преломлением при условии падения света каждый раз на границу раздела под углом Брюстера). Если, например, для стекла (п= 1,53) степень поляриза­ции преломленного луча составляет »15%, то после преломления на 8—10 наложен­ных друг на друга стеклянных пластинок вышедший из такой системы свет будет практически полностью поляризованным. Такая совокупность пластинок называется стопой. Стопа может служить для анализа поляризованного света как при его отраже­нии, так и при его преломлении.

§ 192. Двойное лучепреломление

Все прозрачные кристаллы (кроме кристаллов кубической системы, которые оптически изотропны) обладают способностью двойного лучепреломления, т. е. раздваивания каждого падающего на них светового пучка. Это явление, в 1669 г. впервые обнаружен­ное датским ученым Э. Бартолином (1625—1698) для исландского шпата (разновид­ность кальцита СаСОз), объясняется особенностями распространения света в анизот­ропных средах и непосредственно вытекает из уравнений Максвелла.

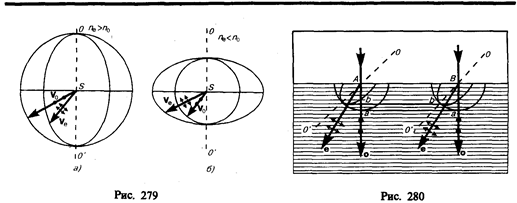
Если на толстый кристалл исландского шпата направить узкий пучок света, то из кристалла выйдут два пространственно разделенных луча, параллельных друг другу и падающему лучу (рис. 277). Даже в том случае, когда первичный пучок падает на кристалл нормально, преломленный пучок разделяется на два, причем один из них является продолжением первичного, а второй отклоняется (рис. 278). Второй из этих лучей получил название необыкновенного (e), а первый — обыкновенного (о).

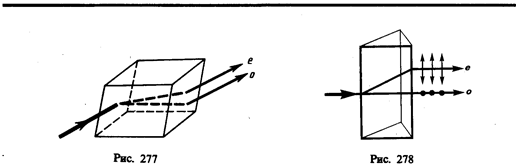
В кристалле исландского шпата имеется единственное направление, вдоль которого двойное лучепреломление не наблюдается. Направление в оптически анизотропном кристалле, по которому луч света распространяется, не испытывая двойного луче­преломления, называется оптической осью кристалла. В данном случае речь идет именно о направлении, а не о прямой линии, проходящей через какую-то точку кристалла. Любая прямая, проходящая параллельно данному направлению, является оптической осью кристалла. Кристаллы в зависимости от типа их симметрии бывают одноосные и двуосные, т.е. имеют одну или две оптические оси (к первым и относится исландский шпат).

Исследования показывают, что вышедшие из кристалла лучи плоскополяризованы во взаимно перпендикулярных плоскостях. Плоскость, проходящая через направление луча света и оптическую ось кристалла, называется главной плоскостью (или главным сечением кристалла). Колебания светового вектора (вектора напряженности Е элект­рического поля) в обыкновенном луче происходят перпендикулярно главной плоскости, в необыкновенном — в главной плоскости (рис. 278).

Неодинаковое преломление обыкновенного и необыкновенного лучей указывает на различие для них показателей преломления. Очевидно, что при любом направлении обыкновенного луча колебания светового вектора перпендикулярны оптической оси кристалла, поэтому обыкновенный луч распространяется по всем направлениям с оди­наковой скоростью и, следовательно, показатель преломления n_o для него есть вели­чина постоянная. Для необыкновенного же луча угол между направлением колебаний светового вектора и оптической осью отличен от прямого и зависит от направления луча, поэтому необыкновенные лучи распространяются по различным направлениям с разными скоростями. Следовательно, показатель преломления п_e необыкновенного луча является переменной величиной, зависящей от направления луча. Таким образом, обыкновенный луч подчиняется закону преломления (отсюда и название «обыкновен­ный»), а для необыкновенного луча этот закон не выполняется. После выхода из кристалла, если не принимать во внимание поляризацию во взаимно перпендикуляр­ных плоскостях, эти два луча ничем друг от друга не отличаются.

Как уже рассматривалось, обыкновенные лучи распространяются в кристалле по всем направлениям с одинаковой скоростью v_o=c/n_o, а необыкновенные — с разной скоростью v_e=с/п_e (в зависимости от угла между вектором Е и оптической осью). Для луча, распространяющегося вдоль оптической оси, n_o=n_e, v_o=v_e, т.е. вдоль оптической оси существует только одна скорость распространения света. Различие в v_e и v_o для всех направлений, кроме направления оптической оси, и обусловливает явление двойного лучепреломления света в одноосных кристаллах.

Допустим, что в точке S внутри одноосного кристалла находится точечный источ­ник света. На рис. 279 показано распространение обыкновенного и необыкновенного лучей в кристалле (главная плоскость совпадает с плоскостью чертежа, OO' — направ­ление оптической оси). Волновой поверхностью обыкновенного луча (он распространя­ется с v_o=const) является сфера, необыкновенного луча (v_e¹const) — эллипсоид враще­ния. Наибольшее расхождение волновых поверхностей обыкновенного и необыкновен­ного лучей наблюдается в направлении, перпендикулярном оптической оси. Эллипсоид и сфера касаются друг друга в точках их пересечения с оптической осью OO'. Если v_e<v_o (n_e>n_o), то эллипсоид необыкновенного луча вписан в сферу обыкновенного луча (эллипсоид скоростей вытянут относительно оптической оси) иодноосный кристаллназываетсяположительным (рис. 279, а). Если v_e>v_o (n_e<n_o), то эллипсоид описан вокруг сферы (эллипсоид скоростей растянут в направлении, перпендикулярном оп­тической оси) и одноосный кристалл называется отрицательным (рис. 279, б). Рассмот­ренный выше исландский шпат относится к отрицательным кристаллам.

В качестве примера построения обыкновенного и необыкновенного лучей рассмот­рим преломление плоской волны на границе анизотропной среды, например положи­тельной (рис. 280). Пусть свет падает нормально к преломляющей грани кристалла, а оптическая ось OO' составляет с нею некоторый угол. С центрами в точках А и В по­строим сферические волновые поверхности, соответствующие обыкновенному лучу, и эллипсоидальные — необыкновенному лучу. В точке, лежащей на OO', эти поверх­ности соприкасаются. Согласно принципу Гюйгенса, поверхность, касательная к сфе­рам, будет фронтом (а—а) обыкновенной волны, поверхность, касательная к эллипсо­идам, — фронтом (b—b) необыкновенной волны. Проведя к точкам касания прямые, получим направления распространения обыкновенного (о) и необыкновенного (е) лу­чей. Таким образом, в данном случае обыкновенный луч пойдет вдоль первоначаль­ного направления, необыкновенный же отклонится от первоначального направления.

§ 193. Поляризационные призмы и поляроиды

В основе работы поляризационных приспособлений, служащих для получения поляри­зованного света, лежит явление двойного лучепреломления. Наиболее часто для этого применяютсяпризмыиполяроиды. Призмы делятся на два класса:

1) призмы, дающие только плоскополяризованный луч(поляризационные призмы);

2) призмы, дающие два поляризованных во взаимно перпендикулярных плоскостях луча (двоякопреломляющие призмы).

Поляризационные призмы построены по принципу полного отражения (см. § 165) одного из лучей (например, обыкновенного) от границы раздела, в то время как другой луч с другим показателем преломления проходит через эту границу. Типичным пред­ставителем поляризационных призм является призма Ни2коля*, называемая часто ни2колем. Призма Николя (рис. 281) представляет собой двойную призму из исландс­кого шпата, склеенную вдоль линии АВ канадским бальзамом с п=1,55. Оптическая ось ОО' призмы составляет с входной гранью угол 48°. На передней грани призмы естественный луч, параллельный ребру СВ, раздваивается на два луча: обыкновенный (n_о=1,66) и необыкновенный (n_e=1,51). При соответствующем подборе угла падения, равного или большего предельного, обыкновенный луч испытывает полное отражение (канадский бальзам для него является средой оптически менее плотной), а затем поглощается зачерненной боковой поверхностью СВ. Необыкновенный луч выходит из кристалла параллельно падающему лучу, незначительно смещенному относительно него (ввиду преломления на наклонных гранях АС и BD).

* У. Николь (1768—1851) — шотландский ученый.

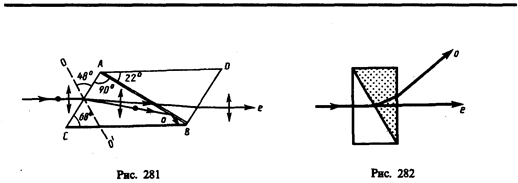
Двоякопреломляющие призмы используют различие в показателях преломления обыкновенного и необыкновенного лучей, чтобы развести их возможно дальше друг от друга. Примером двоякопреломляющих призм могут служить призмы из исландского шпата и стекла, призмы, составленные из двух призм из исландского пшата со взаимно перпендикулярными оптическими осями. Для первых призм (рис. 282) обыкновенный луч преломляется в шпате и стекле два раза и, следовательно, сильно отклоняется, необыкновенный же луч при соответствующем подборе показателя преломления стекла n (n»n_e) проходит призму почти без отклонения. Для вторых призм различие в ориентировке оптических осей влияет на угол расхождения между обыкновенным и необыкновенным лучами.

Двоякопреломляющие кристаллы обладают свойством дихроизма, т. е. различного поглощения света в зависимости от ориентации электрического вектора световой волны, и называются дихроичными кристаллами. Примером сильно дихроичного кри­сталла является турмалин, в котором из-за сильного селективного поглощения обык­новенного луча уже при толщине пластинки 1 мм из нее выходит только необыкновен­ный луч. Такое различие в поглощении, зависящее, кроме того, от длины волны, приводит к тому, что при освещении дихроичного кристалла белым светом кристалл по разным направлениям оказывается различно окрашенным.

Дихроичиые кристаллы приобрели еще более важное значение в связи с изобретени­ем поляроидов. Примером поляроида может служить тонкая пленка из целлулоида, в которую вкраплены кристаллики герапатита (сернокислого иод-хинина). Герапатит — двоякопреломляющее вещество с очень сильно выраженным дихроизмом в об­ласти видимого света. Установлено, что такая пленка уже при толщине »0,1 мм полностью поглощает обыкновенные лучи видимой области спектра, являясь в таком тонком слое совершенным поляризатором. Преимущество поляроидов перед призмами — возможность изготовлять их с площадями поверхностей до нескольких квадрат­ных метров. Однако степень поляризации в них сильнее зависит от l, чем в призмах. Кроме того, их меньшая по сравнению с призмами прозрачность (приблизительно 30%) в сочетании с небольшой термостойкостью не позволяет использовать поляро­иды в мощных световых потоках. Поляроиды применяются, например, для защиты от ослепляющего действия солнечных лучей и фар встречного автотранспорта.

Разные кристаллы создают различное по значению и направлению двойное луче­преломление, поэтому, пропуская через них поляризованный свет и измеряя изменение его интенсивности после прохождения кристаллов, можно определить их оптические характеристики и производить минералогический анализ. Для этой цели используются поляризационные микроскопы.

§ 194. Анализ поляризованного света

Пусть на кристаллическую пластинку, вырезанную параллельно оптической оси, нор­мально падает плоскополяризованный свет (рис. 283). Внутри пластинки он разбивает­ся на обыкновенный (о) и необыкновенный (е) лучи, которые в кристалле пространст­венно не разделены (но движутся с разными скоростями), а на выходе из кристалла складываются.

Так как в обыкновенном и необыкновенном лучах колебания светового вектора совершаются во взаимно перпендикулярных направлениях, то на выходе из пластинки в результате сложения этих колебаний возникают световые волны, вектор Е (а следо­вательно, и Н) в которых меняется со временем так, что его конец описывает эллипс, ориентированный произвольно относительно координатных осей. Уравнение этого эллипса (см. (145.2)):

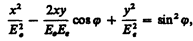(194.1)

где Е_o и Е_e — соответственно составляющие напряженности электрического поля вол­ны в обыкновенном и необыкновенном лучах, j — разность фаз колебаний. Таким образом, в результате прохождения через кристаллическую пластинку плоскополяризованный свет превращается в эллиптически поляризованный.

Между обыкновенным и необыкновенным лучами в пластинке возникает оптичес­кая разность хода

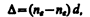
или разность фаз

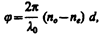
где d — толщина пластинки, l₀ — длина волны света в вакууме.

Если D = (n_o– n_e) d = l/4, j = ±p/2, то уравнение (194.1) примет вид

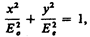
т. е. эллипс ориентирован относительно главных осей кристалла. При E_o=Е_e, (если световой вектор в падающем на пластинку плоскополяризованном свете составляет угол a = 45° с направлением оптической оси пластинки)

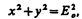
т. е. на выходе из пластинки свет оказывается циркулярно поляризованным.

Вырезанная параллельно оптической оси пластинка, для которой оптическая раз­ность хода

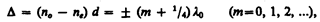
называетсяпластинкой в четверть волны (пластинкой l/4). Знак плюс соответствует отрицательным кристаллам, минус — положительным. Плоскополяризованный свет, пройдя пластинку l/4, на выходе превращается в эллиптически поляризованный (в частном случае циркулярно поляризованный). Конечный результат, как уже рассматри­вали, определяется разностью фаз j и углом a. Пластинка, для которой

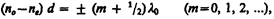
называетсяпластинкой в полволныи т. д.

В циркулярно поляризованном свете разность фаз j между любыми двумя взаимно перпендикулярными колебаниями равна ±p/2. Если на пути такого света поставить пластинку l/4, то она внесет дополнительную разность фаз ±p/2. Результирующая разность фаз станет равной 0 или p. Следовательно (см. (194.1)), циркулярно поляризо­ванный свет, пройдя пластинку l/4, становится плоскополяризованным. Если теперь на пути луча поставить поляризатор, то можно добиться полного его гашения. Если же падающий свет естественный, то он при прохождении пластинки l/4 таковым и оста­нется (ни при каком положении пластинки и поляризатора погашения луча не достичь).

Таким образом, если при вращении поляризатора при любом положении пластинки интенсивность не меняется, то падающий свет естественный. Если интенсивность меняется и можно достичь полного гашения луча, то падающий свет циркулярно поляризованный; если полного гашения не достичь, то падающий свет представляет смесь естественного и циркулярно поляризованного.

Если на пути эллиптически поляризованного света поместить пластинку l/4, оп­тическая ось которой ориентирована параллельно одной из осей эллипса, то она внесет дополнительную разность фаз ±p/2. Результирующая разность фаз станет равной нулю или p. Следовательно, эллиптически поляризованный свет, пройдя пластинку l/4, повернутую определенным образом, превращается в плоскополяризованный и может быть погашен поворотом поляризатора. Этим методом можно отличить эллиптически поляризованный свет от частично поляризованного или циркулярно поляризованный свет от естественного.

§ 195. Искусственная оптическая анизотропия

Двойное лучепреломление имеет место в естественных анизотропных средах (см. § 192). Существуют, однако, различные способы получения искусственной оптической анизотропии, т. е. сообщения оптической анизотропии естественно изотропным веществам.

Оптически изотропные вещества становятся оптически анизотропными под дейст­вием: 1) одностороннего сжатия или растяжения (кристаллы кубической системы, стекла и др.); 2) электрического поля (эффект Керра*; жидкости, аморфные тела, газы); 3) магнитного поля (жидкости, стекла, коллоиды). В перечисленных случаях вещество приобретает свойства одноосного кристалла, оптическая ось которого со­впадает с направлением деформации, электрического или магнитного полей соответст­венно указанным выше воздействиям.

* Д. Керр (1824—1904) — шотландский физик.

Мерой возникающей оптической анизотропии служит разность показателей прело­мления обыкновенного и необыкновенного лучей в направлении, перпендикулярном оптической оси:

(195.1)

где k₁, k₂, k₃ — постоянные, характеризующие вещество, s — нормальное напряжение (см. § 21), Е и Н — соответственно напряженность электрического и магнитного полей.

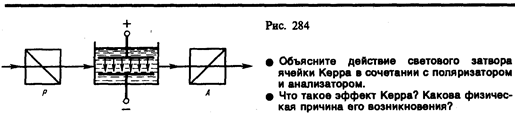
На рис. 284 приведена установка для наблюдения эффекта Керра в жидкостях (установки для изучения рассмотренных явлений однотипны). Ячейка Керра — кювета с жидкостью (например, нитробензолом), в которую введены пластины конденсатора, помещается между скрещенными поляризатором Р и анализатором А. При отсутствии электрического поля свет через систему не проходит. При наложении электрического поля жидкость становится двоякопреломляющей; при изменении разности потенци­алов между электродами меняется степень анизотропии вещества, а следовательно, и интенсивность света, прошедшего через анализатор. На пути l между обыкновенным и необыкновенным лучами возникает оптическая разность хода

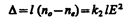
(с учетом формулы (195.1)) или соответственно разность фаз

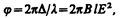
где B=k₂/l — постоянная Керра.

Эффект Керра — оптическая анизотропия веществ под действием электрического поля — объясняется различной поляризуемостью молекул жидкости по разным напра­влениям. Это явление практически безынерционно, т. е. время перехода вещества из изотропного состояния в анизотропное при включении поля (и обратно) составляет приблизительно 10^–10 с. Поэтому ячейка Керра служит идеальным световым затво­ром и применяется в быстропротекающих процессах (звукозапись, воспроизводство звука, скоростная фото- и киносъемка, изучение скорости распространения света и т. д.), в оптической локации, в оптической телефонии и т. д.

Искусственная анизотропия под действием механических воздействий позволяет исследовать напряжения, возникающие в прозрачных телах. В данном случае о степени деформации отдельных участков изделия (например, остаточных деформаций в стекле при закалке) судят по распределению в нем окраски. Так как применяемые обычно в технике материалы (металлы) непрозрачны, то исследование напряжений производят на прозрачных моделях, а потом делают соответствующий пересчет на проектируемую конструкцию.