Основные свойства преобразования Лапласа и Z-преобразования
| Свойства преобразования Лапласа | Свойства Z-преобразования |
1. Свойство линейности:
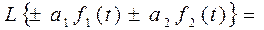 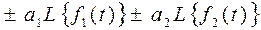
| 1. Свойство линейности:
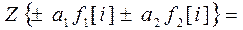 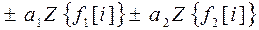
|
2. Теорема о конечном значении:
Если функция s∙F(s) является аналитической в правой полуплоскости и на мнимой оси, то
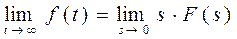
| 2. Теорема о конечном значении:

|
3. Теорема о начальном значении:
Если  , то , то 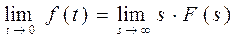
| 3. Теорема о начальном значении:
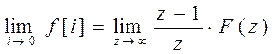
|
4. Теорема сдвига в области вещественной переменной:
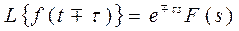 t-τ — запаздывание (по оси вправо). t+τ — упреждение (по оси влево).
t-τ — запаздывание (по оси вправо). t+τ — упреждение (по оси влево).
| 4. Теорема сдвига в области вещественной переменной:
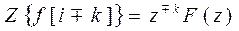 , где k — целое число, кратное периоду дискретности. , где k — целое число, кратное периоду дискретности.
|
5. Свойство дифференцирования:
Если начальные условия нулевые, то 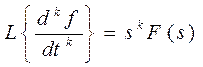
| |
6. Свойство интегрирования:
при нулевых начальных условиях
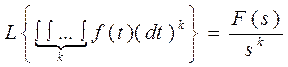
| |
7. Теорема свёртки:
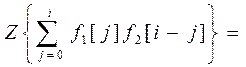
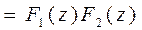
|
Дата добавления: 2015-01-02; просмотров: 895;
