Непрерывные математические модели

Математическая модель системы при этом приводится к стандартному виду (или форме Коши):

(1)

Система уравнений (1) — это уравнение состояния в развёрнутой форме.

Соответствующая системе уравнений (1) структура системы:

В матричной форме систему уравнений (1) можно записать в следующем виде:

(2)

Здесь X, Y — вектора соответственно состояния и управления (смотри выше):

A — матрица системы; B — матрица управления.

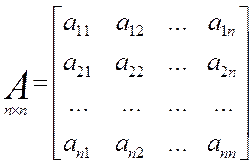
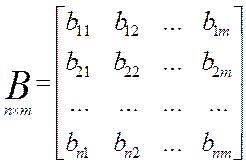
Уравнению состояния (2) соответствует следующая структура системы:

Система уравнений (1) и уравнение (2) соответствуют случаю, когда в качестве выходных переменных рассматриваются все переменные состояния.

В общем же случае количество выходных переменных зависит от рассматриваемой задачи и определяется линейной комбинацией переменных состояний 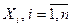и входных переменных (управляющих воздействий) .

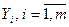Поэтому уравнение состояния системы в развёрнутой форме примет следующий вид:

(3)

Количество выходных переменных 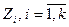зависит от решаемой задачи.

Системе уравнений (3) будет соответствовать следующая структура системы:

В матричной форме уравнение состояния системы выглядит так:

(4)

Уравнению состояния (4) соответствует следующая структура системы:

Z(t) — вектор выхода

С — матрица системы; D — матрица управления.

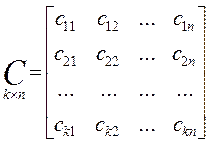
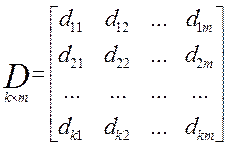
Пример 1.

Записать уравнения состояния в развёрнутой и матричной формах, составить схему (структуру) системы в переменных состояния непрерывной системы, математическая модель которой следующая:

.

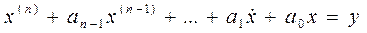Решение.

1. Вводим переменные состояния:

, , …, .

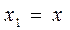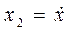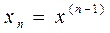2. Запишем уравнение состояния системы в развёрнутой форме Коши:

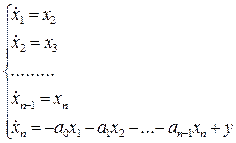
3. Запишем уравнение состояния в матричной форме:

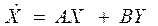
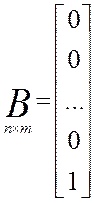
4. Составляем структуру системы в переменных состояния:

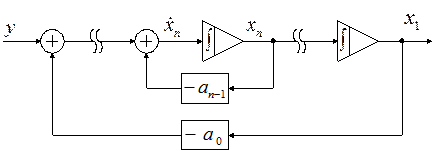
Пример 2.

Смотри условие примера 1, но .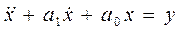

Решение.

1. Вводим переменные состояния:

, .

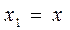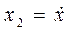2. Запишем уравнение состояния системы в развёрнутой форме Коши:

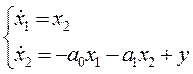
3. Запишем уравнение состояния в матричной форме:

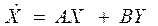
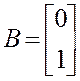
4. Составляем структуру системы в переменных состояния:

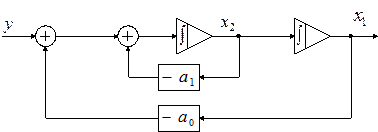
Пример 3.

По структуре системы в переменных состояния записать уравнения состояния в развёрнутой и матричной формах.

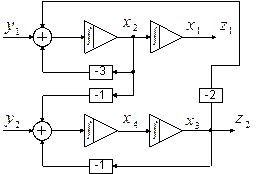
1.)

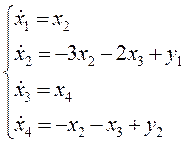
2.)

3.)

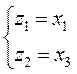
4.)

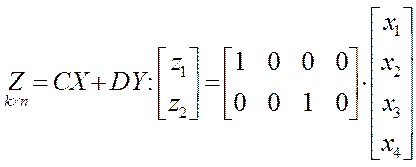
В замкнутой динамической системе выходной сигнал не может появиться на входе мгновенно для противодействия входному сигналу. Это обусловлено тем, что энергия в подсистемах не может изменяться мгновенно, то есть существует запаздывание. Энергия колеблется относительно некоторого уровня и при определённых условиях система из источника подавления колебаний становится их генератором, то есть оказывается неустойчивой.

41. Понятие устойчивости по А. М. Ляпунову(1892 год.)

Рассмотрим непрерывную многомерную систему в свободном движении, математическая модель которой следующая:

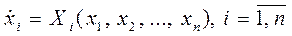… (1)

Здесь X_i — любая линейная или нелинейная функция, а x_i — обобщённая фазовая координата или переменная состояния системы n-мерного порядка (фазовые координаты).

В n-мерном фазовом пространстве (пространстве состояний) в фиксированный момент времени x_i определяют состояние системы в виде точки с соответствующими координатами, например, при n=3:

 

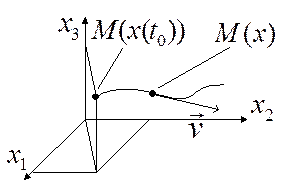
M(x) — изображающая точка. В переходном режиме изображающая точка описывает некоторую траекторию, которую назовём фазовой.

Проекции вектора скорости изображающей точки на оси — левые части уравнений (1), следовательно, о поведении системы в переходном режиме можно судить по правым частям уравнений (1).

Так, например, если n=2, имеем фазовую плоскость:

 

Исключая из этой системы время t, получим: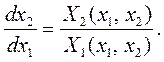

 

Интегрируя это уравнение, получим семейство фазовых траекторий (фазовый портрет) системы, каждая из которых соответствует определённому значению постоянной интегрирования.

Фазовый портрет полностью определяет основные свойства свободного движения системы.

 

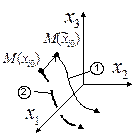
Пусть в начальный момент времени изображающая точка M(xi0) при t=0 начала двигаться по некоторой невозмущённой фазовой траектории и пусть в тот же самый начальный момент времени на неё подействовал мгновенный кратковременный импульс, который сместил эту точку в положение 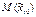. В результате точка M будет двигаться по возмущённой траектории .

 

Таким образом, движение системы устойчиво, если при сдвиге начального положения изображающей точки на величину не более малой положительной величины 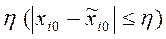(*) возмущённое движение в последующие моменты времени будет отличаться от невозмущённого на величину не более сколь угодно малой величины (**).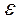

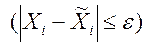В противном случае движение системы не устойчиво.

Если при этом выполняется условие 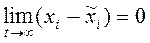(***), то движение асимптотически устойчиво. Следовательно, по Ляпунову оценивается устойчивость системы при достаточно малых начальных отклонениях. Линейная стационарная система, устойчивая “в малом”, будет устойчива и “в большом”.

<31323334353637>

---

Дата добавления: 2015-01-02; просмотров: 1476;

---